2.  Экстремальная характеристика типа
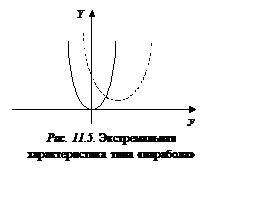
«парабола» изображена на рис. 11.5. В простейшем случае она описывается уравнением
Y = y2.
Экстремальная характеристика типа
«парабола» изображена на рис. 11.5. В простейшем случае она описывается уравнением
Y = y2.
В общем случае уравнение экстремальной характеристики типа «парабола» имеет вид
![]() , (11.3)
, (11.3)
где k1(t) также отражает наклон ветвей параболы; y0(t) – горизонтальный дрейф экстремальной характеристики; Y0(t) – вертикальный дрейф экстремума.
3. Экстремальная характеристика типа «парабола n-го порядка» описывается уравнением
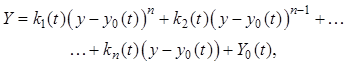
где ki(t) – коэффициенты, которые отражают
наклон ветвей параболы, ![]() ; y0(t) –
горизонтальный дрейф экстремальной характеристики; Y0(t) –
вертикальный дрейф экстремума.
; y0(t) –
горизонтальный дрейф экстремальной характеристики; Y0(t) –
вертикальный дрейф экстремума.
4. Матричное описание экстремальной характеристики имеет вид
![]() . (11.4)
. (11.4)
Зависимость элементов матрицы D(t) отражает изменение во времени параметров экстремальной характеристики.
11.4. Условие экстремума
Рассмотрим экстремальную характеристику произвольного вида
![]() , (11.5)
, (11.5)
полагая для простоты, что отсутствует дрейф экстремума.
Как известно, необходимым условием экстремума является равенство нулю градиента, полученного для этой характеристики [11], т. е. выполнение условия
![]() , (11.6)
, (11.6)
где 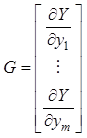 –
градиент (вектор частных производных) выходной переменной объекта.
–
градиент (вектор частных производных) выходной переменной объекта.
Для того чтобы определить тип
экстремума характеристики (11.5), можно задать небольшие приращения по
переменным ![]() относительно значения
относительно значения ![]() в виде
в виде ![]() и
исследовать полученные значения выхода Y. В случае, когда справедливы соотношения
и
исследовать полученные значения выхода Y. В случае, когда справедливы соотношения
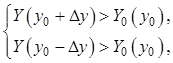 (11.7)
(11.7)
Y0 представляет собой точку минимума.
Если значения выхода Y при небольших отклонениях от Y0 удовлетворяют условиям
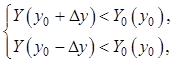 (11.8)
(11.8)
то Y0 соответствует точке максимума характеристики (11.5).
11.5. Постановка задачи синтеза экстремальных систем
Цель экстремального управления состоит в обеспечении минимума или максимума заданной функции качества Y(t,y) при недостаточной априорной информации об объекте.
Задача синтеза экстремальной системы заключается в отыскании для объекта типа (11.1) такого управляющего воздействия u(×), которое позволяло бы автоматически определить положение экстремума и удерживать в нем систему. Математически это означает выполнение условия
![]() , (11.9)
, (11.9)
где ![]() – экстремальное значение выходной
характеристики.
– экстремальное значение выходной
характеристики.
Поскольку экстремальному
значению ![]() соответствует определенное значение
соответствует определенное значение ![]() , задачу синтеза можно переформулировать.
Для экстремального объекта (11.1) необходимо определить управляющее воздействие
u(×), которое обеспечит выполнение
свойства
, задачу синтеза можно переформулировать.
Для экстремального объекта (11.1) необходимо определить управляющее воздействие
u(×), которое обеспечит выполнение
свойства
![]() . (11.10)
. (11.10)
Как видим, задача синтеза
экстремальной системы сводится к задаче стабилизации в точке экстремума ![]() , а для контроля за достижением этой точки
следует использовать условия (11.6) – (11.8).
, а для контроля за достижением этой точки
следует использовать условия (11.6) – (11.8).
Таким образом, при синтезе экстремальных систем от алгоритма управления требуются организация движения в точку экстремума, если градиент выходной характеристики G не равен нулю, и удержание объекта в точке экстремума, если он равен нулю.
Анализ задачи синтеза экстремальных систем управления показывает, что в ней можно выделить три относительно самостоятельные подзадачи:
- задача оценки градиента;
-
организация
движения системы к точке экстремума в соответствии с условием ![]() ;
;
- стабилизация системы в точке экстремума.
Рассмотрим последовательно каждую из них.
11.6. Способы оценки градиента
Задача непрерывной оценки градиента представляет собой самостоятельную и очень непростую техническую проблему. К настоящему времени разработаны различные способы оценки как величины, так и знака градиента [1, 5, 7, 10 – 13]. Остановимся на некоторых из них.
11.6.1. Способ деления производных
Рассмотримсуть данного способа на примере одноканальных объектов со статической экстремальной характеристикой
![]() . (11.11)
. (11.11)
Определим полную производную выходной переменной по времени
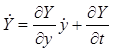 . (11.12)
. (11.12)
Второе слагаемое в выражении (11.12) обусловлено
наличием дрейфа. При медленном дрейфе экстремальной характеристики им можно
пренебречь, так как ![]() . В этом случае из выражения
(11.12) можно определить величину градиента как отношение двух полных
производных по времени:
. В этом случае из выражения
(11.12) можно определить величину градиента как отношение двух полных
производных по времени:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.