 При малой амплитуде поискового сигнала
можно считать, что статическая экстремальная характеристика в малой окрестности
рабочей точки
При малой амплитуде поискового сигнала
можно считать, что статическая экстремальная характеристика в малой окрестности
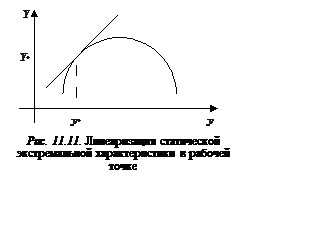
рабочей точки ![]() линейна (рис. 11.11), поэтому
заменим ее касательной. В этом случае уравнение статической экстремальной характеристики
принимает вид
линейна (рис. 11.11), поэтому
заменим ее касательной. В этом случае уравнение статической экстремальной характеристики
принимает вид
![]() , (11.18)
, (11.18)
где k – тангенс угла наклона касательной, который определяется соотношением
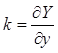 . (11.19)
. (11.19)
Таким образом, k = G. В дальнейшем используем это обозначение.
Сигнал на входе экстремального объекта представляет собой сумму
![]() . (11.20)
. (11.20)
Для простоты будем полагать, что y* = 0 (преобразования не изменятся и в общем случае, но станут более громоздкими). Выражение (11.18) с учетом (11.19) и (11.20) принимает вид
![]() .
(11.21)
.
(11.21)
Запишем теперь выражение для сигнала на выходе ФЧУ:
![]() (11.22)
(11.22)
или с учетом (11.21)
![]() . (11.23)
. (11.23)
Так как усредняющий фильтр усредняет сигналы на периоде, то на его выходе получим
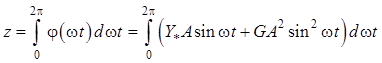 . (11.24)
. (11.24)
Представив в (11.24) интеграл суммы в виде суммы интегралов, запишем
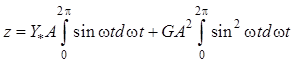 . (11.25)
. (11.25)
Первый интеграл в
выражении (11.25) на периоде будет равен нулю, а во втором ![]() выразим через косинус двойного угла:
выразим через косинус двойного угла:
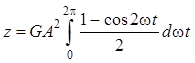 .
.
Полученное выражение преобразуем к виду
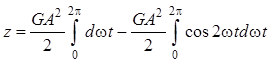 . (11.26)
. (11.26)
Поскольку интеграл ![]() на периоде равен нулю, на выходе фильтра
получим сигнал, пропорциональный градиенту
на периоде равен нулю, на выходе фильтра
получим сигнал, пропорциональный градиенту
![]() . (11.27)
. (11.27)
Метод синхронного детектирования работает устойчиво, хорошо защищен от помех и часто применяется в реальных системах поиска экстремума.
Аналогичный подход можно
использовать и для оценки градиента в многоканальных системах. С этой целью к
каждому значению выходной переменной динамической части объекта ![]() добавляется свой поисковый сигнал определенной
частоты и амплитуды (
добавляется свой поисковый сигнал определенной
частоты и амплитуды (![]() ). В систему необходимо добавить
соответствующее число полосовых фильтров, каждый из которых будет выделять свою
составляющую выходного сигнала
). В систему необходимо добавить
соответствующее число полосовых фильтров, каждый из которых будет выделять свою
составляющую выходного сигнала ![]() . Наличие m усредняющих фильтров позволяет
получить отдельные компоненты вектора
. Наличие m усредняющих фильтров позволяет
получить отдельные компоненты вектора ![]() .
.
11.6.5. Оценка градиента с помощью специального фильтра
Оригинальный способ оценки градиента был разработан на кафедре автоматики НГТУ [5]. Структурная схема устройства (фильтра) оценки частной производной представлена на рис. 11.12.
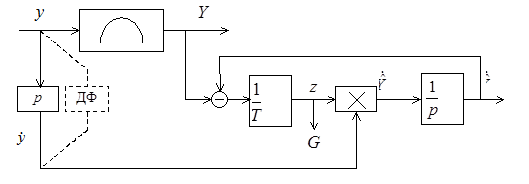 Рис.
11.12. Структурная
схема фильтра оценки градиента
Рис.
11.12. Структурная
схема фильтра оценки градиента
Покажем, что данное устройство действительно позволяет оценивать частную производную. С этой целью для промежуточной переменной z запишем соотношение
![]() , (11.28)
, (11.28)
где ![]() – оценка выходной переменной
экстремального объекта;
T – постоянная времени фильтра.
– оценка выходной переменной
экстремального объекта;
T – постоянная времени фильтра.
Дифференцируя по времени соотношение (11.28), получим уравнение динамики фильтра оценки градиента относительно переменной z
![]() . (11.29)
. (11.29)
Учитывая, что ![]() , представим (11.29) в виде
, представим (11.29) в виде
![]() . (11.30)
. (11.30)
При достаточно малом
значении постоянной времени (![]() ) уравнение (11.30)
вырождается в соотношение
) уравнение (11.30)
вырождается в соотношение
![]() (11.31)
(11.31)
из которого следует
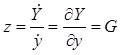 . (11.32)
. (11.32)
Таким образом, предложенное устройство действительно позволяет оценивать частную производную, причем точность оценки будет тем выше, чем меньше параметр T.
На практике необходимую
для оценки градиента производную ![]() рекомендуется
определять с помощью дифференцирующего фильтра (на рис. 11.12 показан
пунктиром), имеющего малую постоянную времени.
рекомендуется
определять с помощью дифференцирующего фильтра (на рис. 11.12 показан
пунктиром), имеющего малую постоянную времени.
11.7. Организация движения к экстремуму
Организация движения к экстремуму в автоматической системе основана на контроле градиента и использовании его в законе управления. Такие системы называются градиентными экстремальными системами (рис. 11.13).
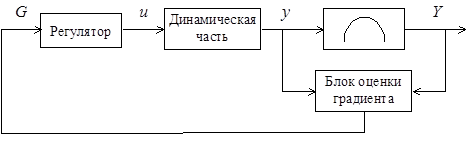
Рис. 11.13. Обобщенная функциональная схема градиентной экстремальной системы
Существующие способы их построения используют как оценку значения градиента (системы с управлением по градиенту) [1, 13], так и оценку знака компонент градиента (системы с запоминанием экстремума, отдельные типы шаговых систем).
11.7.1. Градиентные системы первого порядка
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.