11.7.3. Одноканальные системы общего вида
Обсудим теперь задачу синтеза для объектов управления произвольного порядка, которые описываются нелинейным нестационарным дифференциальным уравнением
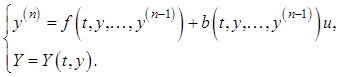 (11.42)
(11.42)
Предполагается,
что дрейф экстремума медленный, т. е. ![]() . В этом случае градиент
определяется соотношением
. В этом случае градиент
определяется соотношением
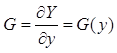 .
.
Сформируем снова пропорциональный градиенту закон управления
![]() (11.43)
(11.43)
и исследуем поведение замкнутой системы
![]() . (11.44)
. (11.44)
Обеспечить устойчивость
замкнутой системы можно соответствующим
выбором коэффициента усиления ![]() . Так как система (11.44) нелинейная, для анализа устойчивости можно использовать второй метод
Ляпунова, на основе которого определяется коэф-фициент
. Так как система (11.44) нелинейная, для анализа устойчивости можно использовать второй метод
Ляпунова, на основе которого определяется коэф-фициент ![]() .
Поскольку второй метод Ляпунова дает лишь достаточное условие
устойчивости, выбранная функция Ляпунова может оказаться неудачной, поэтому
регулярную процедуру расчета регулятора здесь предложить нельзя.
.
Поскольку второй метод Ляпунова дает лишь достаточное условие
устойчивости, выбранная функция Ляпунова может оказаться неудачной, поэтому
регулярную процедуру расчета регулятора здесь предложить нельзя.
11.7.4. Градиентные системы, основанные на методе локализации
Данный способ синтеза экстремальной системы предполагает использование в законе управления действительной и желаемой старшей производных выходной переменной динамической части системы аналогично способу управления нелинейными нестационарными объектами (см. разд. 10).
Рассмотрим возможности метода применительно к объекту управления (11.42), описание которого представим в переменных состояния:
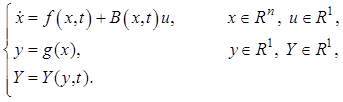 (11.45)
(11.45)
Здесь предполагаем, что
функция ![]() допускает многократное дифференцирование,
а дрейф экстремума достаточно медленный.
допускает многократное дифференцирование,
а дрейф экстремума достаточно медленный.
Цель управления заключается в определении такого управляющего воздействия u = u(×), которое обеспечивает выполнение условия (11.10)
![]()
с заданной точностью ![]() .
.
Наряду с условием статики предъявляются требования и к динамике, т. е. к характеру переходных процессов, в виде оценок
![]() и
и ![]() .
.
Для формирования алгоритма
управления необходимо предварительно определить производную выходных переменных
динамической части объекта, которая непосредственно зависит от управления. При
этом обозначим через C
вектор-строку производных ![]() .
.
Исследуем ситуацию, когда
![]() . (11.46)
. (11.46)
В этом случае от управляющего воздействия будет явно зависеть первая производная выходных переменных динамической части объекта
![]() , (11.47)
, (11.47)
поэтому требования к поведению замкнутой системы следует формировать относительно нее в виде желаемого дифференциального уравнения [4, 12]
![]() , (11.48)
, (11.48)
где a – коэффициент, который выбирается из условия требуемого времени выхода на экстремум. Причем для большого класса объектов типа (11.45) желаемое дифференциальное уравнение можно конструировать в классе линейных уравнений, формируя распределение корней аналогично модальному методу синтеза.
В статике желаемое уравнение (11.48) вырождается в условие
![]() , что соответствует точке экстремума.
, что соответствует точке экстремума.
Зададим закон управления на основе метода локализации в виде
![]() , (11.49)
, (11.49)
где k – коэффициент усиления регулятора.
Использование ![]() в алгоритме управления (11.49) позволяет парировать
влияние динамической части объекта и действующих на него возмущений, а наличие
градиента – организовать движение к точке экстремума, соответствующей точке
равновесия замкнутой системы.
в алгоритме управления (11.49) позволяет парировать
влияние динамической части объекта и действующих на него возмущений, а наличие
градиента – организовать движение к точке экстремума, соответствующей точке
равновесия замкнутой системы.
Подставив (11.49) в (11.47), получим уравнение динамики для выходной переменной ДЧ
![]()
![]() , (11.50)
, (11.50)
которое преобразуется к виду
![]() .
.
При условии, что ![]() , получим уравнение замкнутой системы
, получим уравнение замкнутой системы
![]() . (11.51)
. (11.51)
Начиная с некоторых
значений коэффициента k
выполняется условие ![]() , и уравнение (11.51) при
условии, что
, и уравнение (11.51) при
условии, что ![]() , вырождается в следующее:
, вырождается в следующее:
![]() . (11.52)
. (11.52)
Пренебрегая первым
слагаемым в уравнении (11.52) при ![]() , запишем его в виде
, запишем его в виде
![]() .
.
Таким образом, соответствующий выбор коэффициента усиления регулятора позволяет с заданной точностью обеспечить в замкнутой системе желаемую динамику выхода на экстремум. Параметры регулятора выбираются из соотношения
![]() . (11.53)
. (11.53)
В этом случае ошибка поддержания в системе желаемого уравнения не будет превышать 5...1 %. Структурная схема системы приведена на рис. 11.16.
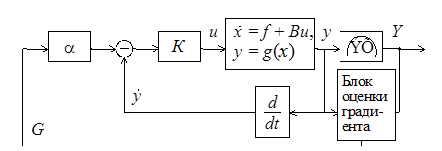
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.