Рис. 11.16. Расчетная схема системы со старшей производной в управлении
В реальной системе для оценки полной производной по времени используется дифференцирующий фильтр, поэтому оценивать градиент удобно с помощью специального фильтра, который будем называть фильтром оценки частной производной.
Следует отметить, что
использование в системе фильтров с малыми инерционностями может приводить к
возникновению в ней разнотемповых процессов, для исследования свойств которых необходимо
применять метод разделения движений (см.
подразд. 9.5). Эти процессы будут различными в зависимости от соотношения
постоянных времени ![]() и
и ![]() . При
соизмеримых инерционностях фильтров в замкнутой системе возникают два вида
движений: быстрые и медленные, причем медленные движения соответствуют системе
с точным законом управления.
. При
соизмеримых инерционностях фильтров в замкнутой системе возникают два вида
движений: быстрые и медленные, причем медленные движения соответствуют системе
с точным законом управления.
Если постоянные времени фильтров различаются на порядок и более, то в системе возникают три вида движений: сверхбыстрые, быстрые и медленные. Сверхбыстрые движения определяются наименьшей постоянной времени фильтров, быстрые движения обусловлены вторым фильтром, а медленные движения, как и в первом случае, являются рабочими и соответствуют системе с точным законом управления.
Пример 11.2
Рассчитать систему поиска экстремума для объекта управления, поведение которого описывают уравнения
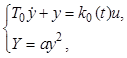
где T0 = 2 c, ![]() , a =
2, y(0) = 1. Необходимо обеспечить выход на экстремум за время
, a =
2, y(0) = 1. Необходимо обеспечить выход на экстремум за время ![]() .
.
На основании требований к динамике
процесса определим желаемый полюс замкнутой системы (![]() )
и сформируем желаемое уравнение того же порядка, что и уравнение объекта
)
и сформируем желаемое уравнение того же порядка, что и уравнение объекта
![]() или
или ![]() , где a = 0,25. Коэффициент усиления регулятора K выбираем из условия
, где a = 0,25. Коэффициент усиления регулятора K выбираем из условия ![]() . В данном случае С = 1,
. В данном случае С = 1, ![]() ,
, ![]() . Следовательно,
К = 40.
. Следовательно,
К = 40.
Для оценки производных используем
дифференцирующий фильтр первого порядка (см. разд. 10) с постоянной времени ![]() с и фильтр оценки частной производной (см.
п. 11.7.5) с постоянной времени
с и фильтр оценки частной производной (см.
п. 11.7.5) с постоянной времени ![]() с (рис. 11.17).
с (рис. 11.17).
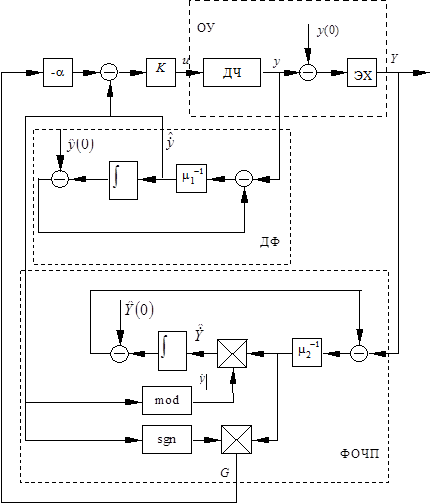
Рис. 11.17. Структурная схема системы к примеру 11.2
Здесь ДЧ – динамическая часть объекта;
ЭХ – экстремальная характеристика; ДФ – дифференцирующий фильтр; ФОЧП – фильтр
оценки частной производной. Блок «mod» реализует операцию получения модуля оценки производной ![]() , а блок «sgn» – ее знака. Эти блоки введены для обеспечения устойчивости
замкнутой системы.
, а блок «sgn» – ее знака. Эти блоки введены для обеспечения устойчивости
замкнутой системы.

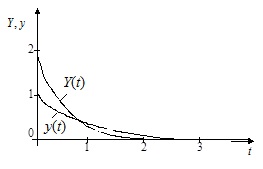
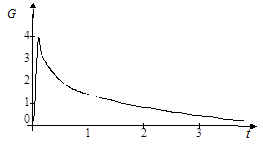
На рис. 11.18 и 11.19 отображены переходные процессы в системе и изменение оценки градиента при согласованных параметрах дифференцирующего фильтра и фильтра оценки частной производной соответственно.
Заключение
Рассмотренные в этом разделе способы организации систем автоматического поиска экстремума являются основными способами синтеза, которые регулярно используются в настоящее время. Здесь представлены как известные подходы (пропорциональный градиенту закон управления), так и оригинальные разработки авторов (метод локализации). Наряду с ними в литературе можно найти множество специальных приемов, которые помогают в частных ситуациях находить удовлетворительные решения.
Для организации движения к экстремуму используется информация о величине или знаке градиента, оценивать который на практике значительно сложнее, чем полную производную по времени. мы обсудили основные подходы к решению данной задачи, включая специальный фильтр оценки частной производной.
Использование метода локализации в совокупности с этим фильтром позволяет синтезировать экстремальные системы с требуемым качеством процесса для широкого класса объектов с нелинейной динамической частью и дрейфующим экстремумом.
Общей
технической трудностью для систем автоматического поиска экстремума является
качество измерения показателя ![]() и
переменных
и
переменных ![]() .
Это обстоятельство прежде всего следует учитывать при выборе или проектировании
системы датчиков.
.
Это обстоятельство прежде всего следует учитывать при выборе или проектировании
системы датчиков.
Задачи
11.1. Структурная схема объекта представлена на рис. 11.20. Рассчитать систему поиска экстремума в предположении, что градиент можно оценить точно.
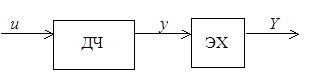
Рис. 11.20. Структурная схема объекта к задаче 11.1
Модель динамической части и
экстремальной характеристики имеет вид ![]() .
Необходимо обеспечить время выхода на экстремум
.
Необходимо обеспечить время выхода на экстремум ![]()
11.2. Модель объекта имеет вид
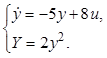
Рассчитать градиентную систему с
точной оценкой ![]() , обеспечивающую выход на
экстремум за время
, обеспечивающую выход на
экстремум за время ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.