Системы автоматического поиска экстремума. Основные понятия и определения. Описание объекта управления. Типовые модели экстремальной характеристики объекта, страница 5

Рассмотрим организацию движения к экстремуму на примере простейшего объекта управления, который описывается следующей системой уравнений:

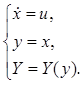                                    (11.33)

Сформируем пропорциональный градиенту закон управления в виде

.                                 (11.34)

Подставив (11.34) в уравнение объекта (11.33), получим уравнение замкнутой системы

,                                 (11.35)

которое представляет собой нелинейное дифференциальное уравнение относительно переменной y. Полагая , запишем уравнение статики

,                                  (11.36)

где зависимость G от t параметрическая. Поскольку , из выражения (11.36) следует

.                                   (11.37)

Таким образом, в случае устойчивости замкнутой системы процессы в ней будут сходиться к точке равновесия, которая является точкой экстремума. Устойчивость движения в замкнутой системе можно обеспечить соответствующим выбором коэффициента усиления , при этом выход на экстремум происходит автоматически. В некоторых случаях с помощью коэффициента  кроме устойчивости можно обеспечить определенную длительность переходного процесса в замкнутой системе, т. е. заданное время выхода на экстремум.

Пример 11.1

Для объекта, математическая модель которого имеет вид

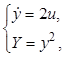
необходимо обеспечить выход на экстремум за заданное время с.

В соответствии с (11.34) сформируем управление

.

Так как известна модель статической экстремальной характеристики, градиент можно определить аналитически,

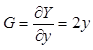, и организовать алгоритм управления в виде

.

В этом случае получим уравнение замкнутой системы

.

Как видим, она имеет первый порядок, и для ее устойчивости корень характеристического уравнения  должен быть отрицательным. Следовательно, необходимо выбирать коэффициент

.

Численное значение определим, используя корневые оценки переходного процесса. Так как , то получим . Если выбрать , то алгоритм управления, обеспечивающий выполнение заданных требований, примет вид

.

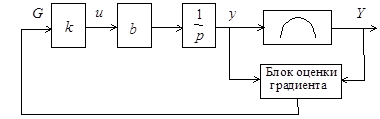
Рис. 11.14. Структурная схема системы для примера 11.1

Структурная схема системы с рассчитанным законом управления представлена на рис. 11.14.

11.7.2. Метод  «тяжелого  шарика»

Рассмотренный в п. 11.8.2 метод позволяет автоматически найти экстремум, в окрестности которого заданы начальные условия. Если экстремальная характеристика помимо глобального имеет также и несколько локальных экстремумов, то система может «остановиться» в любом из них.

По аналогии с тяжелым шариком, который скатывается в овраг, проскакивая локальные экстремумы, данный метод предполагает введение в систему дополнительной инерционности для придания процессам свойства «проскакивать» точки локальных экстремумов.

Будем рассматривать объект, поведение которого описывают уравнения (11.33). Чтобы обеспечить колебательные переходные процессы в системе, добавим в обратную связь апериодическое звено с постоянной времени T, которую и определим в результате синтеза.

Расчетная структурная схема такой системы приведена на рис. 11.15.

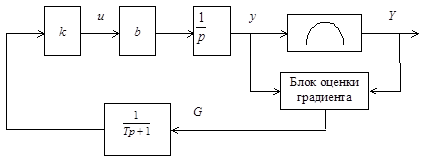
Рис. 11.15. Структурная схема системы с дополнительной инерционностью

Запишем операторное уравнение замкнутой системы, предполагая, что с помощью соответствующего блока градиент можно оценить точно,

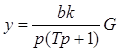,                                 (11.38)

где  так как экстремальная характеристика описывается уравнением .

Преобразуем уравнение (11.38) к виду

, которое затем представим в стандартной форме

.                        (11.39)

Отсюда следует, что, выбирая  можно обеспечить устойчивость системы (11.39), уравнение статики которой имеет вид

.                                  (11.40)

Таким образом, точка равновесия  эквивалентна точке экстремума, так как при этом .

Характер движения системы к точке экстремума определяется характеристическим уравнением

.                              (11.41)

Выбирая распределение корней из условия обеспечения требуемых показателей качества процесса выхода на экстремум ( и ), сформируем желаемое характеристическое уравнение второго порядка. Приравнивая коэффициенты при соответствующих степенях оператора pэтих двух уравнений (согласно методике модального метода синтеза), можно определить требуемые численные значения kи T.