Оптимальные системы. Основные понятия. Постановка задачи синтеза оптимальных систем. Метод динамического программирования, страница 5

При ограниченном ресурсе (например, ) вычисленное с помощью (12.35) оптимальное управляющее воздействие может находиться вне области допустимых значений, поэтому для отыскания максимума гамильтониана необходимо использовать максимальное значение управления .

12.4.2. Процедура  определения  оптимального управления

На основе рассмотренных соотношений принципа максимума Л.С. Понтрягина можно предложить следующую процедуру расчета регулятора.

1. Описание объекта следует привести к стандартному для теории оптимального управления виду (12.1):

.

Записывается критерий оптимальности (12.4) в форме

.

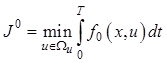2. Формируется расширенный вектор состояния  и правых частей в общем виде записывается вектор сопряженных координат

.

3. В форме скалярного произведения векторов  и  записывается гамильтониан

.

4. Из условия максимума гамильтониана определяется оптимальное управление как функция сопряженных координат

.

5. Формируется система дифференциальных уравнений для нахождения сопряженных координат

.

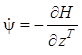6. Вычисляется оптимальное управление в виде функции времени (программное управление)

.

7. По возможности осуществляется переход к оптимальному управлению в виде обратной связи

.

Рассмотрим вычисление оптимального управления с помощью описанной процедуры на примере.

Пример 12.3

Определить оптимальное управление для объекта, поведение которого описывают уравнения

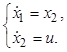
Требуется обеспечить переход из начальной точки в конечную

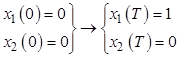, за заданное время с при минимуме затрат энергии, т. е.

.

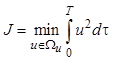Поскольку известно описание объекта в переменных состояния, переходим к формированию расширенного вектора состояния и правых частей, а также запишем вектор сопряженных координат

 , ,

.

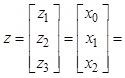
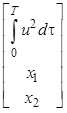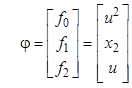Сформируем теперь гамильтониан

и определим его максимум по u

.

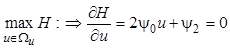Из этого уравнения определим оптимальное управление в виде функции сопряженных координат

.

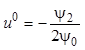Для сопряженных координат запишем систему дифференциальных уравнений

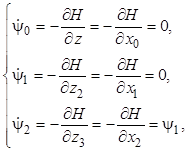     из которой определим

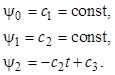
В результате оптимальное управление принимает вид

.

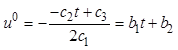Коэффициенты  определим, решая краевую задачу. С этой целью запишем уравнения замкнутой системы

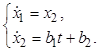
Определим решение для переменных состояния в виде

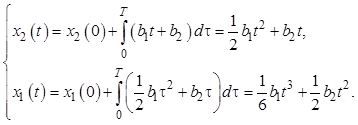
Учтем теперь заданные начальные и конечные условия и T = 1 с.

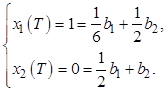
Решая полученную систему уравнений, определим неизвестные коэффициенты: . В результате оптимальный программный закон управления имеет вид

.

12.4.3. Задача  оптимального  быстродействия

Задача оптимального быстродействия имеет некоторые особенности, которые упрощают ее решение на основе принципа максимума Л.С. Понтрягина [1, 2].

Гамильтониан быстродействия. Рассмотрим общий класс объектов управления (12.1)

с ограниченным управлением () и критерием оптимальности в виде (12.6), т. е. критерием быстродействия

.

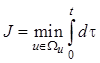Согласно процедуре синтеза на основе принципа максимума запишем расширенный вектор правых частей и вектор сопряженных координат

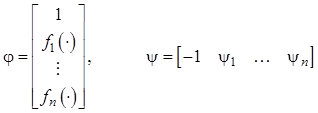, а затем сформируем гамильтониан в виде

.       (12.36)

В соответствии с (12.33) максимум гамильтониана равен нулю. Поскольку первое слагаемое в данном выражении не зависит от управления, можно вместо (12.35) рассматривать усеченный гамильтониан, который называется гамильтонианом быстро-действия

.                 (12.37)

В этом случае уравнение принципа максимума принимает вид

.                                       (12.38)

Таким образом, при решении задачи оптимального быстродействия нет необходимости переходить к расширенному вектору состояния и расширенному вектору правых частей. Можно сформировать гамильтониан быстродействия и определить управление, обеспечивающее его максимум в соответствии с (12.38).

Разрывное управление. для объектов с аддитивным управлением вида (12.2)

, ограниченным ресурсом управления  и требованием в виде критерия быстродействия управляющее воздействие имеет разрывной характер.

Сформируем гамильтониан быстродействия (12.37)

,         (12.39)

где  – i-й элемент вектора , а  – i-я строка матрицы , i = 1,2,…,n.

Управление, обеспечивающее максимум гамильтониана (12.39) с учетом ограничений, имеет вид

.                                 (12.40)

Следовательно, для объектов класса (12.2) оптимальное управление всегда носит релейный характер.

Теорема о числе переключений.Данная теорема связывает число переключений оптимального управления со свойствами объекта. Она справедлива для линейных объектов (12.3)