Оптимальные системы. Основные понятия. Постановка задачи синтеза оптимальных систем. Метод динамического программирования, страница 3

12.3. Метод  динамического  программирования

Метод динамического программирования, предложенный в начале 50-х годов Р. Беллманом [1, 2, 12, 14], используется для синтеза оптимальных систем управления. Он базируется на вариационном исчислении, при выводе его основных соотношений используется принцип оптимальности.

12.3.1. Принцип  оптимальности

Формулировка принципа оптимальности следующая: конечный участок оптимальной траектории есть также оптимальная траектория. Доказательство этого принципа можно найти в [1], здесь ограничимся лишь его пояснением.

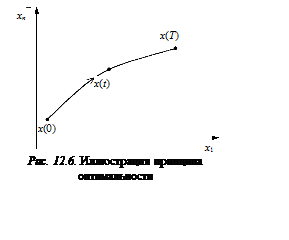
Предположим, что существует единственная оптимальная траектория перехода из точки x(0) в точку x(T) (рис. 12.6). Промежуточная точка x(t) разбивает эту траекторию на две части. Причем ее конечный участок представляет собой оптимальную траекторию, иначе можно было бы найти новую оптимальную траекторию перехода из точки x(t) в точку x(T) и организовать движение из начальной точки x(0) в конечную x(T) по новой оптимальной траектории. Это невозможно, так как для системы существует лишь одна оптимальная траектория перехода из одной точки в другую.

12.3.2. Основные  соотношения  метода  динамического  программирования

Будем рассматривать общий класс объектов управления, который описывается уравнением (12.1)

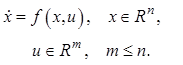
Полагаем, что переменные состояния  и ресурс управления  ограничены.

Необходимо определить управляющее воздействие, которое обеспечивало бы переход из начального состояния x(t) в конечное x(T) за время T (рис. 12.7) в соответствии с критерием оптимальности

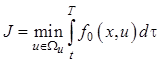.                             (12.12)

Выберем на оптимальной траектории перехода промежуточную точку x(t+Dt), расположенную достаточно близко к заданной начальной точке. Согласно принципу оптимальности конечный участок есть также оптимальная траектория, поэтому представим критерий оптимальности (12.12) в виде суммы двух критериев, соответствующих двум участкам движения,

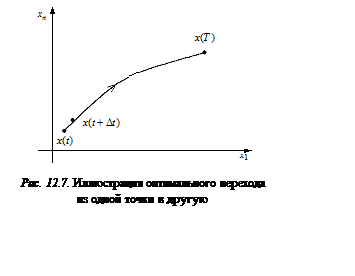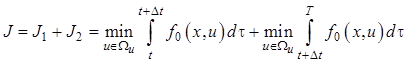     (12.13)

или после преобразований

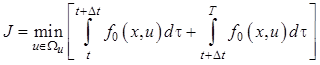.            (12.14)

Рассматривая второй интеграл выражения (12.14) как функцию нижнего предела, обозначим его

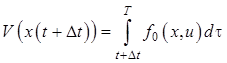.                     (12.15)

С учетом (12.15) соотношение (12.14) представим в виде

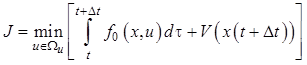.          (12.16)

Полагая промежуток времени Dt достаточно малым, сделаем в (12.16) следующие упрощения:

1) интеграл приближенно заменим произведением

;                        (12.17)

2) функцию  разложим в ряд Тейлора в окрестности заданной начальной точки

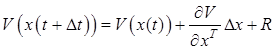,                (12.18)

где R – остаточные члены ряда разложения, которыми можно пренебречь.

Учитывая приближенные замены (12.17) и (12.18), преобразуем выражение (12.16):

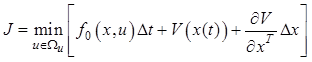.         (12.19)

Представим  в равенстве (12.19) в виде суммы двух составляющих следующим образом:

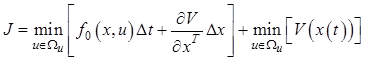.   (12.20)

Обсудим получившееся выражение. Согласно введенному обозначению (12.15) здесь

,                           (12.21)

поэтому вместо (12.20) получим

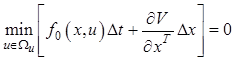.                   (12.22)

Поделим обе части равенства (12.22) на Dt

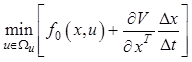, а затем устремим Dt ® 0 и получим следующее уравнение:

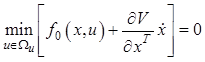.                    (12.23)

Поскольку рассматривается оптимальная траектория движения для объекта (12.1), подставим в (12.23) вместо  правую часть уравнения объекта и получим основное уравнение метода динамического программирования в виде

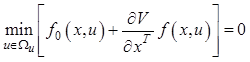.           (12.24)

Таким образом, оптимальным будет управление, которое минимизирует выражение (12.24). Однако использовать его для вычисления  нельзя, так как одно уравнение (12.24) содержит m+1 неизвестную величину ( и ).

12.3.3. Расчетные  соотношения  метода  динамического  программирования

В случае оптимального управления  соотношение (12.24) принимает вид

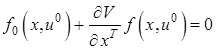.             (12.25)

Продифференцируем (12.25) по  вдоль оптимальной траектории

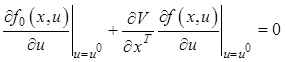.         (12.26)

Добавив уравнения (12.26) к (12.25), получим систему из m+1 уравнения с m+1 неизвестным, решая которую можно найти оптимальное управление.