![]() ,
, ![]() ,
, ![]() ,
, ![]()
с ограничением типа ![]() и критерием быстродействия. При этом оптимальное
управление имеет вид (12.40).
и критерием быстродействия. При этом оптимальное
управление имеет вид (12.40).
Поскольку объект управления линейный, для него можно определить корни характеристического уравнения
![]() (12.41)
(12.41)
в виде совокупности ![]() .
.
Рассмотрим без доказательства формулировку теоремы.
Теорема. если корни характеристического уравнения (12.41) вещественные, то число переключений управляющего воздействия не превышает (n – 1), где n – порядок объекта.
Следствие. число интервалов постоянства управляющего воздействия не превышает n.
Варианты изменения оптимального управления в линейной системе третьего порядка с вещественными корнями приведены на рис.12.8.
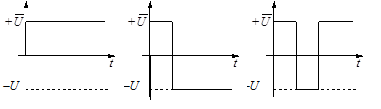
а б в
Рис. 12.8. Иллюстрация изменения оптимального управления:
а – нет переключений; б – с одним, в – с двумя переключениями
В случае, когда среди совокупности корней характеристического уравнения (12.41) есть комплексно-сопряженные, число переключений теоретически не ограничено. В реальных системах невысокого порядка число переключений, как правило, невелико.
Пример 12.4
Рассмотрим задачу синтеза оптимальной по быстродействию системы для объекта
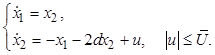
Запишем гамильтониан быстродействия
![]()
и определим оптимальное управление
![]() .
.
Система дифференциальных уравнений для сопряженных координат имеет вид
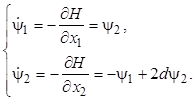
Ее можно представить в виде одного дифференциального уравнения
![]() , которому соответствует
характеристическое
, которому соответствует
характеристическое
![]() .
.
При d³ 1 его корни l1 и l2 будут вещественными и положительными, следовательно, оптимальное управление принимает вид
![]() , где
, где ![]() .
.
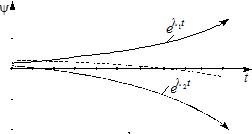

а б
Рис. 12.9. Иллюстрация теоремы о числе переключений:
а – одно переключение; б – без переключений; штриховая линия – сумма экспонент
Сумма двух экспонент может только один раз изменить знак, что соответствует однократному переключению управляющего воздействия (рис. 12.9,а), либо не изменит знака совсем. В последнем случае не будет переключений управляющего воздействия (рис. 12.9,б).
12.5. Метод поверхности переключения
12.5.1. Основные понятия
Этот метод применяется для формирования оптимального управления в виде обратной связи в случае, когда управление носит разрывный (релейный) характер.
Рассматриваются общая задача синтеза оптимальной системы для объекта (12.1)
![]()
и переход из
произвольных начальных состояний ![]() в заданные конечные
в заданные конечные ![]() в соответствии с некоторым критерием оптимальности
в соответствии с некоторым критерием оптимальности
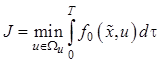 . (12.42)
. (12.42)
Оптимальный закон управления в этом случае имеет вид
![]() , (12.43)
, (12.43)
где ![]() – вектор максимальных значений управления,
– вектор максимальных значений управления,
![]() – вектор функций, определяющих в
пространстве состояний некоторую поверхность, которая называется поверхностью
переключения [13]
– вектор функций, определяющих в
пространстве состояний некоторую поверхность, которая называется поверхностью
переключения [13]
![]() . (12.44)
. (12.44)
Для определения этой поверхности предварительно конечная точка «приводится» к началу координат с помощью замены переменных
![]() . (12.45)
. (12.45)
Затем в пространстве состояний
исследуются траектории перехода из произвольных начальных состояний ![]() в конечную точку
в конечную точку![]() .
На траекториях перехода выделяются точки, где происходит смена знака
управления, которые объединяются в поверхность переключения
.
На траекториях перехода выделяются точки, где происходит смена знака
управления, которые объединяются в поверхность переключения
![]() .
(12.46)
.
(12.46)
 Однако
чтобы получить траекторию перехода из начальной точки
Однако
чтобы получить траекторию перехода из начальной точки ![]() в
начало координат пространства состояний, необходимо также задавать в
соответствии с принципом максимума и начальные условия для сопряженных
координат
в
начало координат пространства состояний, необходимо также задавать в
соответствии с принципом максимума и начальные условия для сопряженных
координат ![]() . Если эти начальные условия выбраны
неудачно, то получим траекторию перехода не в
. Если эти начальные условия выбраны
неудачно, то получим траекторию перехода не в ![]() , а в
произвольную точку пространства состояний. В этом случае следует задать новые
начальные условия
для сопряженных координат
, а в
произвольную точку пространства состояний. В этом случае следует задать новые
начальные условия
для сопряженных координат ![]() и вновь попытаться
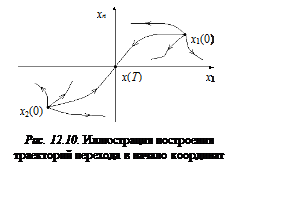
отыскать траекторию перехода в начало координат (рис.12.10).
и вновь попытаться
отыскать траекторию перехода в начало координат (рис.12.10).
Для новой
начальной точки ![]() траектория перехода в начало
координат также может быть получена в результате перебора начальных условий для
сопряженных координат (рис.12.10).
траектория перехода в начало
координат также может быть получена в результате перебора начальных условий для
сопряженных координат (рис.12.10).
Объединяя точки переключения управления
на всех траекториях перехода из произвольных состояний в начало координат,
можно получить поверхность переключения в виде (12.46) или, разрешив уравнение
(12.46) относительно ![]() , в следующей форме:
, в следующей форме:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.