Оптимальные системы. Основные понятия. Постановка задачи синтеза оптимальных систем. Метод динамического программирования, страница 8

Оптимальный закон управления следующий:

.

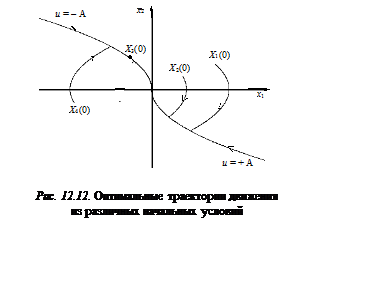
Теперь изменим направление движений на противоположное, т. е. вернемся к обычному времени (рис. 12.12).

Оптимальные траектории движения системы представляют собой участки парабол (рис. 12.12). Если начальная точка не принадлежит линии переключений, то в системе может быть только одно переключение управления (точки X₁(0), X₂(0) и X₄(0)). Переключений не будет совсем, если начальная точка находится на линии переключений (начальные условия X₃(0)).

12.6. Субоптимальные  системы

Субоптимальными будем называть системы, которые близки по свойствам к оптимальным с заданной точностью. Точность приближения к оптимальной системе определяется соотношением

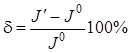,                              (12.49)

где  – критерий, соответствующий субоптимальной системе.

Такую систему получают в результате либо аппроксимации оптимального закона управления, либо искусственного ограничения рабочей области пространства состояний.

Рассмотрим оптимальный закон управления

.

Поверхность переключения сложной конфигурации можно аппроксимировать, например, следующим образом:

,                         (12.50)

представить в виде совокупности функций

                       (12.51)

или аппроксимировать каким-либо другим способом. При этом будут получаться субоптимальные системы, с различной степенью точности близкие к оптимальным.

Обсудим особенности субоптимальных систем на примере.

Пример 12.6

Рассмотрим оптимальную по быстродействию систему (см. пример 12.5) и аппроксимируем линию переключения прямой (рис. 12.13).

Уравнение реальной линии переключения имеет вид

.

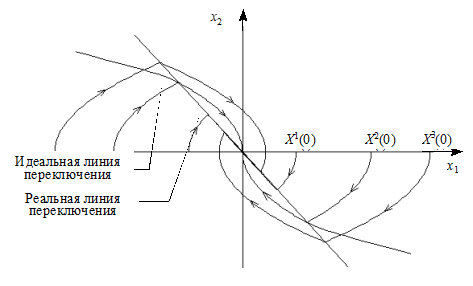
Рис. 12.13. Фазовый портрет субоптимальной системы к примеру 12.6

Процессы в субоптимальной системе будут существенно зависеть от начальных условий. Так, при движении из X¹(0) изображающая точка системы попадает на реальную линию переключений , а затем движется вдоль нее в скользящем режиме.

Из начальных условий X ²(0) изображающая точка системы будет попадать в точку пересечения идеальной и реальной линий переключения и к началу координат будет двигаться по соответствующему участку идеальной линии переключений, т. е. по оптимальной траектории.

При движении из X ³(0) изображающая точка системы будет доходить до , переключаться на траекторию, соответствующую другому знаку управления, вновь попадать на реальную линию переключений и двигаться вдоль нее в скользящем режиме.

Таким образом, в субоптимальной системе могут быть строго оптимальные процессы, только если из начальных условий изображающая точка системы по фазовой траектории попадает в точку пересечения идеальной и реальной линий переключения.

заключение

С появлением рассмотренных методов оптимизации переходных процессов в теории автоматического управления возник ряд инженерных методов проектирования. Особенно распространенными стали релейные системы оптимизации по быстродействию. В начале раздела рассмотрен случай системы первого порядка, когда алгоритм оптимального управления практически не зависит от параметров объекта и возмущения. К сожалению, этот случай крайне редкий; в подавляющем большинстве система автоматики должна парировать действие возмущений, и вид оптимальных процессов, а следовательно, и алгоритм управления зависят от возмущений. При этом характер изменения самих возмущений во времени неизвестен. Это обстоятельство резко снизило интерес инженеров к математическим методам оптимального управления.

Есть однако несколько конкретных технических ситуаций, когда возможности математической теории оптимального управления могут использоваться в полной мере. Показательным примером может служить задача автоматического управления лифтами и подъемниками. При этом параметры объекта (масса груза) меняются от процесса к процессу, а ограниченным является только значение старшей производной от положения (выходной величины). Старшей производной является ускорение кабины лифта или какая-либо его производная. В пассажирских подъемниках они должны быть ограничены условиями комфорта пассажиров, а в грузовых – условиями прочности конструкции (ограничен должен быть рывок).

В целом теория оптимальных систем автоматики уже вошла в классику автоматического управления, и для нее существует сфера применения, хотя и не такая большая, как казалось вначале.