Оптимальные системы. Основные понятия. Постановка задачи синтеза оптимальных систем. Метод динамического программирования, страница 4

Поскольку (12.25) и (12.26) представляют собой систему уравнений в частных производных, для определения из нее оптимального управления, как правило, приходится использовать приближенные численные методы. В результате найденное управление получается не оптимальным, а близким к нему.

Задача отыскания точного оптимального управления методом динамического программирования носит название задачи АКОР (аналитического конструирования оптимальных регуляторов). Эта задача имеет решение при наличии следующих условий [1, 2, 13]:

1.  Объект управления описывается линейным уравнением состояния (12.3)

,    , , .

2.  Переход из начальной точки  в конечную  рассматривается на бесконечном интервале времени.

3.  Критерий оптимальности имеет вид квадратичной формы (12.11)

.

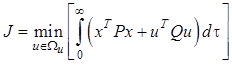Оптимальное управление, полученное методом динамического программирования, для такой постановки задачи будет иметь вид

.

Таким образом, оптимальным для задачи АКОР будет пропорциональный закон управления.

Пример 12.2

Объект, модель которого имеет вид

необходимо перевести из начальной точки  в конечную . Время процесса не ограничено, а критерий оптимальности следующий:

.

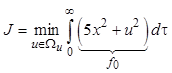Запишем основное уравнение метода динамического программирования (12.25)

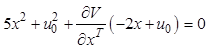
и дополним его уравнением в частных производных (12.26)

.

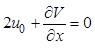Выразим из второго уравнения  и подставим в первое, в результате получим

или после приведения подобных

.

Решение квадратного уравнения относительно управления дает два значения

Поскольку для одной системы двух оптимальных законов управления быть не может, одно из найденных значений не является оптимальным. Для определения оптимального управления проверим устойчивость замкнутой системы.

В уравнение объекта подставим значение  и получим уравнение замкнутой системы

.

Как видим, система неустойчива, а значит, первое управляющее воздействие не является оптимальным.

В уравнение объекта подставим значение , при этом уравнение замкнутой системы примет вид

и она будет устойчивой.

Таким образом, оптимальный закон управления имеет вид , где .

12.4. Принцип  максимума  Л.С. Понтрягина

12.4.1. Основное  соотношение  принципа  максимума

Принцип максимума Л.С. Понтрягина представляет собой метод расчета оптимального управления. Он был сформулирован независимо [1, 2, 10] и почти в то же время, что и метод динамического программирования. Впоследствии оказалось, что уравнения одного метода можно получить из другого и наоборот. Запишем основные соотношения принципа максимума на основе уравнений метода динамического программирования.

Рассмотрим основное соотношение (12.24)

.

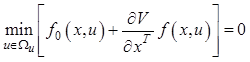Поскольку минимум функции равен максимуму этой же функции с противоположным знаком, запишем его в виде

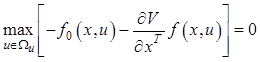.         (12.27)

Преобразуем уравнение (12.27), предварительно введя ряд обозначений.

1. Введем расширенный вектор состояния , дополнив его компонентой x₀:

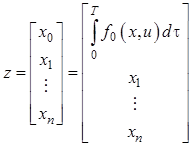.                       (12.28)

2. Введем соответствующий расширенный вектор правых частей :

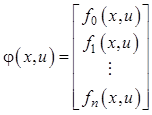.                               (12.29)

3. Вектор сопряженных координат :

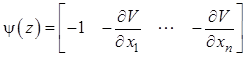.                 (12.30)

Определим скалярное произведение вектора сопряженных координат и расширенного вектора правых частей, которое называется гамильтонианом

.                         (12.31)

Если вместо вектора сопряженных координат и расширенного вектора правых частей подставить их значения согласно (12.30) и (12.29) в выражение (12.31), то последнее можно представить следующим образом:

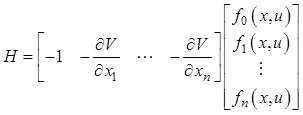
или окончательно

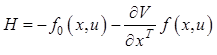.                  (12.32)

С учетом (12.32) уравнение (12.27) можно записать в виде

,                           (12.33)

которое и представляет собой основное соотношение принципа максимума.

При этом сопряженные координаты определяются системой дифференциальных уравнений

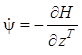.                                   (12.34)

Формулировка принципа максимума. Оптимальным является управление из области допустимых значений, которое обеспечивает максимум гамильтониана (12.33).

В случае, когда ресурс управления объекта не ограничен, для нахождения максимума гамильтониана можно воспользоваться необходимым условием экстремума

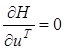.                                  (   12.35)