Оптимальные системы. Основные понятия. Постановка задачи синтеза оптимальных систем. Метод динамического программирования, страница 7

,                                  (12.47)

где  – «усеченный» вектор состояния (без последней компоненты).

С учетом (12.47) оптимальный закон управления (12.43) можно записать в виде

.                        (12.48)

Таким образом, метод поверхности переключения позволяет получить оптимальный закон управления в виде обратной связи. Однако при этом приходится рассматривать две совокупности начальных условий: для переменных состояния  и сопряженных координат , что существенно затрудняет определение управляющего воздействия.

Отметим также, что метод поверхности переключений можно применять для решения задачи оптимального быстродействия при наличии объектов с аддитивным управлением, поскольку в этом случае оптимальное управление всегда будет иметь релейный характер (12.40).

12.5.2. Метод  обратного  времени

С целью упрощения задачи определения поверхности переключения предлагается поменять местами начальную  и конечную  точки, что в пространстве состояний соответствует движению в обратную сторону. Для динамической системы это означает замену времени t на –t . При этом вместо двух совокупностей начальных условий  нужно рассматривать только одну – , так как .

Постановка задачи синтеза оптимальной системы в обратном времени формулируется следующим образом. Для объекта

с ограниченным ресурсом управления необходимо определить оптимальное управление в виде обратной связи, которое обеспечивает переход из начальной точки  в конечную  в соответствии с критерием оптимальности (12.4). При этом заранее известно, что оптимальное управление имеет релейный характер.

Отметим, что в этом случае необходимо перебирать только одну совокупность начальных условий . Причем каждому конкретному значению  соответствует оптимальная траектория перехода из заданной начальной точки  в некоторую конечную . В соответствии с методом поверхности переключений в пространстве состояний на траекториях перехода выделяются точки, где происходит смена знака управления и объединяются в поверхность .

В обычном времени следует изменить направление движения на противоположное. В результате находится оптимальное управление в виде (12.43)

или в форме (12.48).

Пример 12.5

Рассмотрим процедуру определения оптимального управления методом обратного времени для объекта

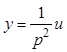
с ограничением на управление . Необходимо перейти из начальной точки  в конечную  с критерием оптимальности

.

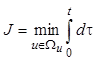запишем уравнения объекта в переменных состояния

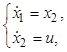
где .

Поскольку рассматривается задача оптимального быстродействия, оптимальное управление носит релейный характер

.

Для определения  в виде функции переменных состояния используем метод поверхностей переключения. Предварительно запишем уравнения объекта в обратном времени

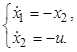
Будем рассматривать следующую задачу перехода: . Для получения фазовых траекторий в пространстве состояний воспользуемся методом непосредственного интегрирования, рассмотрим последовательно два значения оптимального управления.

1.  Случай, когда . Уравнения замкнутой системы имеют вид

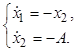
Интегрируя последовательно второе, а затем первое уравнения, получим

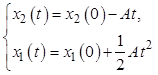
или при нулевых начальных условиях

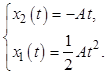
Теперь исключим время, , и запишем уравнение фазовой траектории, выходящей из начала координат при положительном управлении,

.

2.  Случай, когда . При этом уравнения замкнутой системы следующие:

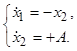
После интегрирования имеем

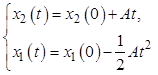
или

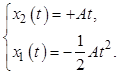
Исключая время, , получим

.

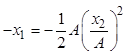В этом случае уравнение фазовой траектории, выходящей из начала координат при отрицательном управлении, принимает вид

.

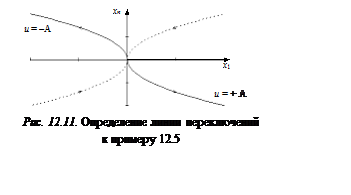
Для каждой фазовой траектории (рис. 12.11) определим направление движения и оставим ту половину параболы, которая соответствует движению из начала координат. Затем объединим эти две полутраектории в одну и получим уравнение линии переключения в виде

.