Отметим, что множество начальных состояний объекта W[x(0)], как правило, совпадает с пространством состояний, а множество конечных состояний W[x(T)] всегда является подмножеством пространства состояний. Кроме этого, объект управления нужно перевести не в любую точку пространства состояний, а лишь в ту, которая принадлежит подмножеству реализуемых равновесных состояний (см. подразд. 10.2).
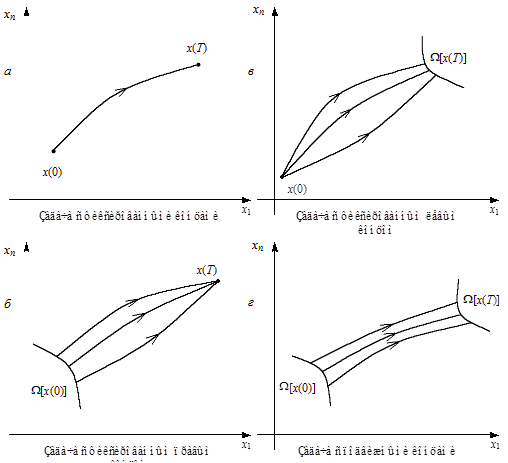
Рис. 12.4. Иллюстрация четырех типов задач синтеза:
с фиксированными концами (а), с одним правым (б), левым (в); задача с подвижными концами (г)
Рассмотрим на примере определение реализуемых равновесных состояний объекта.
Пример 12.2
Определить множество равновесных состояний для объекта, поведение которого описывает система уравнений
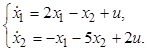
Запишем для него уравнения статики
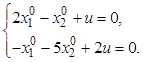
Определим управляющее воздействие из первого уравнения и подставим во второе. После преобразования получим уравнение множества реализуемых равновесных состояний в виде
![]() .
.
Графической интерпретацией этого множества в пространстве состояний является прямая, именно ей должно принадлежать конечное состояние объекта. В другую точку пространства состояний его перевести невозможно (точнее, перевести можно, но стабилизировать нельзя).
12.2.3. Ограничения на переменные состояния и управление
Любая задача оптимизации имеет практический смысл только при ограничениях на переменные состояния и ресурс управления объекта.
Ограничения на переменные состояния
дают некоторую рабочую область Wx в пространстве состояний (рис. 12.5,а).
Наиболее часто они носят характер модуля, ![]() .
.
На управляющие воздействия также
накладываются ограничения, которые в общем случае можно представить в виде
некоторой рабочей области Wu (рис. 12.5,б). В реальных системах ограничение
на ресурс управления, как правило, также носит характер ограничения по модулю ![]() .
.
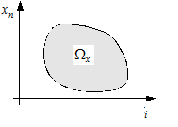

Рис. 12.5. Иллюстрация рабочих областей: переменных состояния (а) и управляющих воздействий (б)
На этапе постановки задачи синтеза необходимо убедиться в том, что множество начальных W[x(0)] и конечных W[x(T)] состояний объекта находится внутри рабочей области пространства состояний Wx.
12.2.4. Критерий оптимальности
Критерий оптимальности в обобщенной форме отражает требования к качеству переходных процессов замкнутой системы. В задаче синтеза оптимальных систем его принято представлять в виде интегрального функционала
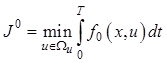 , (12.4)
, (12.4)
где T – заданное время перехода из начального состояния в конечное.
В зависимости от требований к качеству работы системы можно выделить несколько наиболее часто встречающихся критериев оптимальности.
1. Критерий быстродействия отражает требование минимизации времени переходного процесса и может быть записан в виде
![]() . (12.5)
. (12.5)
Критерий (12.5) представим в форме интегрального функционала
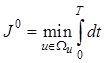 . (12.6)
. (12.6)
2. Критерий минимума затрат энергии по состоянию. В случае, когда требуется минимизировать затраты энергии только по одной из компонент вектора состояния, критерий оптимальности имеет вид
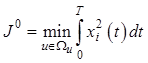 . (12.7)
. (12.7)
Если речь идет о минимизации затрат энергии по всему вектору состояния, то он принимает форму
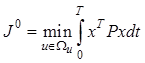 , (12.8)
, (12.8)
где P – матрица коэффициентов квадратичной формы размера ![]() .
.
3. Критерий минимума затрат энергии на управление. Он может быть записан аналогично (12.7) относительно одной из компонент управляющего воздействия
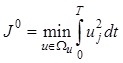 (12.9)
(12.9)
или относительно всего вектора управления
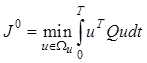 , (12.10)
, (12.10)
где Q – матрица квадратичной формы размера ![]() .
.
4. Критерий минимума полных затрат энергии. Это общий случай критерия минимума затрат энергии, объединяющий критерии (12.8) и (12.9):
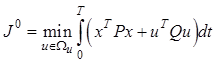 . (12.11)
. (12.11)
12.2.5. Форма результата
При постановке задачи заранее оговаривается тип управляющего воздействия, которое необходимо определить в процессе синтеза. Например, для одноактных систем, работающих без помех и возмущений, можно рассчитывать программное оптимальное
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.