Оптимальные системы. Основные понятия. Постановка задачи синтеза оптимальных систем. Метод динамического программирования, страница 9

12.1. Для объекта, поведение которого описывают уравнения

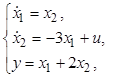
определить оптимальное управление, обеспечивающее переход из начального состояния  в заданное конечное   за время T = 1 с. Критерий оптимальности следующий: .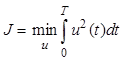

12.2. Для объекта, поведение которого описывают уравнения

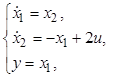
определить оптимальное управление, обеспечивающее переход из начального состояния  в заданное конечное   за минимальное время и при ограниченном управлении .

12.3. Для объекта, математическая модель которого имеет вид

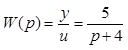, определить оптимальное управление, обеспечивающее переход из начального состояния  в заданное конечное   за время T = 1 с. Критерий оптимальности следующий: .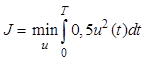

12.4. Определить оптимальное управление, обеспечивающее переход из начального состояния  в заданное конечное  за минимальное время и при ограниченном управлении , для объекта, математическая модель которого имеет вид

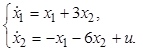
12.5. Определить оптимальное управление, обеспечивающее переход из начального состояния  в заданное конечное  за время T = 1 с, для объекта, математическая модель которого имеет вид

.

Критерий оптимальности .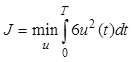

12.6. Для объекта, математическая модель которого имеет вид

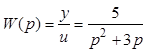, определить оптимальное управление, обеспечивающее переход из начального состояния  в заданное конечное  за минимальное время и при ограниченном управлении .

литература

1.  Александров А.Г. Оптимальные и адаптивные системы. – М.: Высш. шк., 1989.

2.  Атанс М., Фалб П. Оптимальное управление. – М., 1969.

3.  Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. – М.: Наука, 1974.

4.  Востриков А.С. Синтез нелинейных систем методом локализации. – Новосибирск: Изд-во Новосиб. ун-та, 1990.

5.  Востриков А.С., Французова Г.А. Экстремальные и оптимальные системы автоматического управления.: Учеб. пособие. – Новосибирск: НГТУ, 2001.

6.  Геращенко Е.И., Геращенко С.М. Метод разделения движений и оптимизация нелинейных систем. – М.: Наука, 1975.

7.  Иванов В.А., Фалдин Н.В. Теория оптимальных систем автоматического управления. – М., 1981.

8.  Изерман Р. Цифровые системы управления: Пер. с англ. – М., 1984.

9.  Коновалов Г.Н. Радиоавтоматика: Учеб. для вузов по спец. «Радиотехника». – М.: Высш. шк., 1990.

10.  Математическая теория оптимальных процессов / Л.С. Понтрягин,В.Г. Болтянский, Р.В. Гамкрелидзе, Е.Ф. Мищенко. – М.: Наука, 1983.

11.  Олейников В.А., Зотов Н.С., Пришвин А.М. Основы оптимального и экстремального управления. – М.: Высш. шк., 1969.

12.  Ту Ю. Современная теория управления. – М.: Мир, 1971.

13.  Уткин В.И. Скользящие режимы в задачах оптимизации и управления. – М., 1981

14.  Чураков Е.П. Оптимальные и адаптивные системы. – М.: Энергоатомиздат, 1987.

послесловие

Так как вы  не можете иметь все, что хотите,

то желайте только  то, что можете иметь.

Теренций

Об изучении теории автоматического регулирования

В представленном читателю учебном пособии изложены основы дисциплины, которую, как правило, называют теорией автоматического управления. Однако для названия пособия мы применили термин «теория автоматического регулирования». Это объясняется тем, что целью управления в подавляющем большинстве случаев является приведение выхода объекта к нужному значению. Эту частную задачу управления называют процессом регулирования.

Читатель уже заметил, что в теории автоматического регулирования  в полной мере используется язык математики. В этом отношении теория автоматического регулирования подобна таким классическим дисциплинам, как теоретическая механика или теоретическая физика. Математический аппарат в теории автоматического регулирования активно используется с начала ее развития. Не случайно поэтому создателями теории автоматического регулирования мы считаем физика Дж.К. Максвелла, математиков И.А. Вышнеградского, А.М. Ляпунова и многих других. И все же теория автоматического регулирования – сугубо техническая дисциплина. Нельзя стать специалистом по теории автоматического регулирования, изучая только ее математические методы. Применение любой математической конструкции должно иметь технический смысл. И при математическом формулировании задач по анализу или синтезу систем автоматического регулирования центральной должна быть техническая сторона функционирования системы автоматики. Как нам кажется, именно отрыв математической конструкции от технической сути привел к появлению некоторых расхожих понятий, которые, вообще говоря, не имеют осмысленной технической интепретации. Например, часто авторы монографий и даже учебников под «идеальным переходным процессом» понимают мгновенный перевод объекта из начального состояния в конечное. В отличие от математика инженер должен понимать, что для совершения такого процесса при любом физическом объекте управления требуется бесконечно большой импульс энергии. Специалисту никогда не придет в голову требовать такого переходного процесса или пытаться его организовать. Не случайно поэтому мы взяли в качестве эпиграфа к этому разделу изречение, которое приписывают древнему философу Теренцию.