Авторегрессионая модель представляет наибольший интерес. В ней будущее значение процесса выражается через конечную линейную или нелинейную взвешенную сумму предыдущих значений и отклонение (остаток) e.
Линейный прогнозатор имеет вид:
; 
= d1 + d2x(i) + d3x(i
– 1) + ... + dpx(i – p – 1), (37)
где d1, … dр – коэффициенты, определяемые, например, методом наименьших квадратов; i = 1, 2, …, р + 1, … .
Пример реализации алгоритма прогнозирования на основе авторегрессии приведен на рисунке 9.
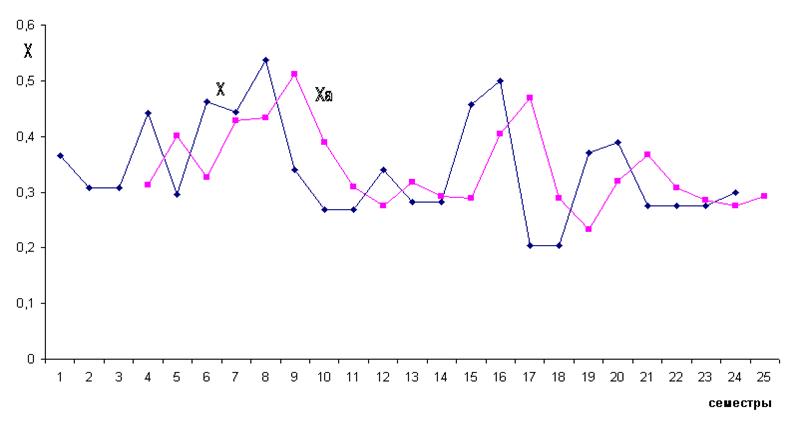Рисунок 9
– Изменения фактических (Х) и прогнозных Ха
(по авторегрессии) значений показателя качественной
успеваемости
1.3 Прогнозирование с использованием адаптивных моделей
1.3.1 Адаптивная селективная модель [15]
Вполне естественно, что нестационарный случайный процесс, представленный в виде временного ряда данных, время от времени претерпевает коренные изменения. Изменяется средний уровень и динамические свойства ряда, причем на одних участках сохраняется приблизительно постоянный уровень, на других ряд растет с определенной скоростью или характеризуется появлением ускорения. Поэтому всякая попытка подобрать какую-либо одну прогнозную модель для всего ряда приводит к чрезмерным ошибкам прогнозирования.
Предположим, что рассматриваемый процесс (ряд данных) генерируется моделью с постоянным средним уровнем, моделью с линейным ростом и квадратичной моделью поочередно. Учитывая это, построим трехструктурную адаптивную комбинированную модель (АКМ), которая включает в свой набор три модели: линейного роста, экспоненциально-взвешенной средней и квадратичную.
Вычисление будущих значений ряда осуществляется по каждой из них в отдельности, но в качестве прогноза берется лучший на данном этапе прогноз. В общем случае при выборе лучшего прогноза нельзя исходить из последней ошибки прогнозирования. Необходимо учитывать некоторую предысторию ошибок. Рассмотрим два варианта селекции( отбора вариантов):
- по критерию 
, согласно которому переключение
на данную модель осуществляется тогда, когда k ее предыдущих
прогнозов являются лучшими по сравнению с прогнозами по другим моделям, входящим
в АКМ;
- по критерию 
, согласно которому переключение
на данную модель осуществляется тогда, когда ее экспоненциально сглаженный
квадрат ошибки прогнозирования минимален в сравнении с аналогичным показателем
для остальных моделей в базовом наборе АКМ.
Эти два критерия характеризуют инерционность переключения. Следует отметить, что общий теоретический анализ эффективности АКМ методом математического анализа затруднителен, и решающее слово остается за машинным экспериментом.
1.3.2 Адаптивная гибридная модель [15]
Для тех случаев, когда входящие в АКМ модели дают сравнительно близкие результаты и селекция затруднена, можно предложить гибридную АКМ, прогноз по которой является взвешенной суммой прогнозов, полученных по входящим в нее предикатам. Вес прогнозов рекомендуется брать адаптивным, обратно пропорциональным экспоненциально-сглаженной квадратичной ошибке.
В отличие от селективной, гибридная модель осуществляет переключение более плавно, со множеством промежуточных положений. В результате получается непрерывный спектр возможных значений прогноза.
При автоматическом формировании базовый набор предикторов не является раз и навсегда определенным. Если с течением времени меняется соотношение между средними квадратами ошибок, то меняется и базовый набор. Таким образом, при прогнозировании модель подвергается двум испытаниям: одно, основанное на анализе средних квадратов прошлых ошибок, дает ответ на вопрос о целесообразности включения модели в базовый набор предикатов; другое, путем сравнения текущих свойств по критерию Q2, определяет ту модель из базового набора, от которой можно ждать наилучшего прогноза.
Построение адаптивных моделей – процедура трудоемкая и реализуется на ЭВМ. В то же время применение адаптивных моделей значительно повышает точность прогноза, уменьшает ошибку прогнозирования.
1.3.3 Трехструктурный прогнозатор Чоу
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.