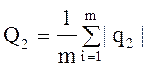Типовые алгоритмы экстраполяционного прогнозирования: Учебно-методическое пособие по дисциплине «Методы и алгоритмы прогнозирования в системах управления», страница 14

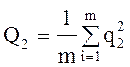     или                                            (65)

2.3  Критерий сложности

Сложность алгоритма может быть оценена количеством математических операций, необходимых для его реализации; временем реализации алгоритма; параметрами его структуры; объемом памяти компьютера, необходимым для реализации алгоритма.

Все математические операции можно разделить на несколько уровней сложности j{1,2,3,4,5},

1 – сложение, сравнение, вычитание;

2 – умножение, деление;

3 – возведение в степень, извлечение корня;

4 – интегрирование, дифференцирование;

5 – определение логарифмов, тригонометрических функций.

Элементарными математическими операциями являются сложение и сравнение.

Время реализации алгоритма может быть рассчитано по формуле:

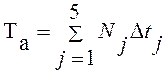                                                                        (66)

где  – количество операций алгоритма, относящихся j-ому уровню сложности;

Dt_j – средняя продолжительность выполнения операции j-ого уровня.

Следует заметить, что формула (66) является упрощенной и не учитывает неарифметические операции: такие как пересылки, обращения к запоминающим устройствам, трансляция с входного языка и т.д.

Другая формула для оценки времени реализации алгоритма:

                                                                                  (67)

где – количество элементарных операций алгоритма, определение которого является весьма трудоемкой задачей;

– время выполнения одной элементарной операции, определяемое быстродействием компьютера.

В.Т. Кулик в работе [2] предлагает рассчитывать сложность алгоритма по следующей формуле:

 Q₃ = a_NN_a + a_ПП_a + a_ММ_a                                                        (68)

где a_N, a_П, a_М – весовые коэффициенты, сумма которых равна 1;

N_a – количество элементарных операций;

П_a –  связность, которая оценивается максимальным числом промежуточных операций, удерживаемых в памяти, при выполнении алгоритма и массивом входных данных;

М_а – точность расчетов при реализации алгоритма.

Для рассматриваемого класса задач, решаемых с применением настольных компьютеров, связность практически не имеет значения, т.е. П_a » 0.

Тогда сложность алгоритма можно считать по упрощенной формуле:

= a_N + a_М                                                                 (69)

где  и  – нормированные (нормализованные) значения критериев М и N. Нормирование может осуществляться, например, по следующим формулам:

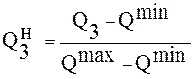 при Q3 → max;

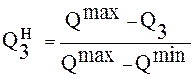 при Q3→min ,                                           (70)

где  – нормированный показатель.

2.4  Комплексный критерий качества прогнозирования

В работе [1] рекомендуется использовать следующий комплексный критерий рекуррентного типа:

Q(i) = bQ(i – 1) + a[q₁(i) + gq₂(i)],                                        (71) где a, b, g – настроечные коэффициенты.

Численное значение весового коэффициента g  выбирается в зависимости от важности q₂(i) по отношению к q₁(i).

Более сложный комплексный критерий, включающий три выше  рассмотренных частных критерия Q1, Q2,Q3 , имеет вид:

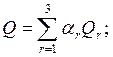
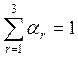 , где - коэффициент важности (весовой коэффициент) r-го критерия, который определяется на основе опроса экспертов.

3  Анализ эффективности алгоритмов экстраполяционного

прогнозирования

3.1  Постановка задачи

Дано:

1)  Анализируемые алгоритмы (см. п. 1);

2)   Характерные ряды модельных или натуральных данных (например, ежемесячный процент % брака проволочного стана за 1990 – 1993 г., приведенный в таблице 7);

3)   Критерий эффективности алгоритмов: гладкость, точность, сложность (см. п. 2);

4)  Метод анализа: на основе моделирования, которое заключается в непосредственной реализации алгоритмов на конкретных выборках и эмпирической оценки значений критериев эффективности.

Требуется:

1)  Оценить критерии эффективности алгоритмов;

2)  Сравнить эффективность алгоритмов.

3.2 Пример анализа алгоритмов

Дано:

1) Анализируемые алгоритмы: скользящего среднего (см. п. 1.1.1.), медианно-экспоненциального сглаживания (см. п. 1.1.4.), экспоненциального сглаживания первого порядка (см. п. 1.1.2.).