Типовые алгоритмы экстраполяционного прогнозирования: Учебно-методическое пособие по дисциплине «Методы и алгоритмы прогнозирования в системах управления», страница 13

1.5.2.2  Сущность и конкретизация алгоритма МЛЭ

1. Для построения алгоритма экстраполяции введем два линейных параметризованных пространства.

 

а) – пространство ситуаций; б) – пространство решений

Рисунок 12 – Экстраполяция по двум обучающим векторам на плоскости

Далее предположим, что известны проектные ситуации Х₁ и Х₂, которым в пространстве решений соответствуют решения у₁ и у₂. Дана новая проектная ситуация Х₃ и нужно найти для нее решение У₃, располагая указанной информацией.

Через известные ситуации х₁ и х₂ проведем прямую линию, являющуюся подпространством проектных ситуаций.

                                      (55)

или в данном случае

 ,                                         (56)

где l – коэффициент пропорциональности.

2. Отображаем пространство {Х¢} параметров на пространство {У¢} результирующих характеристик

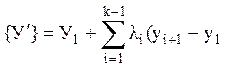                                      (57)

или в данном случае

                                          (58)

3. Определим коэффициенты

 где

                               (59)

 .           (60)

4. Определим решение у₃ для проектной ситуации х₃.

Для новой проектной ситуации х₃ определим ближайшую точку на подпространстве {Х¢}, для чего опустим перпендикуляр из точки х₃ на линию . Получим точку , являющуюся отображением точки х₃ на {Х¢}, которая делит отрезок [х₁, х₂] в определенной пропорции. Разделив отрезок [у₁, у₂] в пространстве {У¢} в той же пропорции получим проектное решение у₃, соответствующее ситуации х₃. в общем случае для нахождения вектора у_i+1 пользуются формулой:

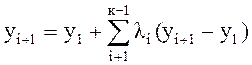                                        (61)

1.5.2.3  Пример реализации алгоритма

Дано: таблица результатов испытаний базы данных АСУ ЗАКАЗ (см. табл.6).

Здесь х₁; х₂ х₃ х₄ представляют собой координаты векторов параметров базы данных.

Причем: х₁ – общее количество сегментов;

х₂ – количество корневых сегментов;

х₃ – количество связей;

х₄ – общее количество сегментов в базе данных;

у – время выполнения одного запроса пользователя.

Требуется: найти оценку  для данного варианта базы данных.

Решение:

Таблица 6 – Результаты испытаний базы данных АСУ ЗАКАЗ

Параметры	х1	х2	х3	х4	у
вариант 1	9	1	8	2995	16,6
вариант 2	14	3	13	3010	19,4
вариант 3	12	2	11	3000	12,7

Определим l для этого случая

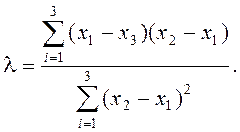
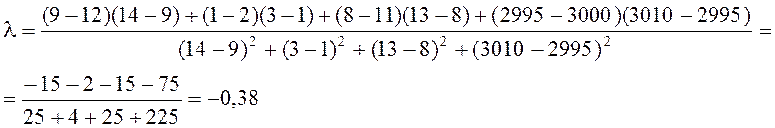
 = у₁ + l(у₂ – у₁);  = 16,6 – 0,38(19,4 – 16,6) = 16,6 – 1 = 15,6.

2  Критерии качества прогнозирования

     2.1  Критерии точности

В качестве критерия точности обычно рассматривается средняя модульная или средняя квадратичная ошибка прогнозирования. При этом среднее определяется на новой выборке данных, называемой контрольной выборкой.

Критерий точности характеризует степень близости прогнозных оценок к фактическим или действительным значениям, появляющимся спустя некоторое время.

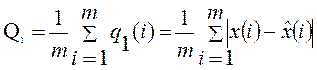                                               (62)

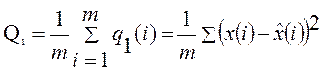                                              (63)

где  - модуль или квадрат ошибки прогнозирования;

m – объем контрольной выборки.

К фактическим значениям здесь относятся отсчеты исходного ВРД, являющиеся результатом измерений. Они включают в себя помеховые составляющие. К действительным значениям относятся такие отсчеты, из которых исключены помеховые составляющие.

Возможно применение и других точностных критериев, например частоты попадания прогнозных оценок в заданную окрестность ±e фактических или действительных значений прогнозируемой переменной

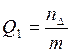, где - количество случаев попадания прогноза в диапазон x(i) ±e.

2.2  Критерии гладкости

Он характеризует плавность изменения прогнозируемых последовательностей и может быть определен через модуль или квадрат первых или вторых разностей  q₂(i) прогнозных оценок. Например, для вторых разностей имеем:

q₂(i) = | – 2+ | или q₂(i) = ( – 2+ )²                                     (64)

Соответственно средние выборочные оценки этого критерия будут равны: