Исходные данные
приведены в таблице 2. Начальные условия: ![]() (3)
= med{х(1); х(2); х(3)} =
(3)
= med{х(1); х(2); х(3)} = ![]() (1)
=
(1)
= ![]() (2). Настроечные коэффициенты: М =
3; a = 0,5. Результаты расчета приведены в таблице 4.
(2). Настроечные коэффициенты: М =
3; a = 0,5. Результаты расчета приведены в таблице 4.
Таблица 4 – Пример расчета по алгоритму медианно-экспоненциального сглаживания
|
Коэффициент расхода металла |
Δх(i) |
Δ |
|
Коэффициент расхода металла |
Δх(i) |
Δ |
|
|
1,139 |
1,088 |
0,050 |
1,088 |
1,098 |
1,096 |
0,001 |
1,096 |
|
1,045 |
1,090 |
-0,045 |
1,09 |
1,110 |
1,097 |
0,013 |
1,097 |
|
1,088 |
1,090 |
-0,002 |
1,09 |
1,105 |
1,103 |
0,001 |
1,104 |
|
1,040 |
1,098 |
-0,049 |
1,089 |
1,014 |
1,104 |
-0,091 |
1,105 |
|
1,089 |
1,066 |
0,022 |
1,066 |
1,010 |
1,105 |
-0,095 |
1,105 |
|
1,147 |
1,065 |
0,081 |
1,066 |
1,048 |
1,059 |
-0,012 |
1,06 |
|
1,045 |
1,076 |
-0,032 |
1,077 |
1,003 |
1,014 |
-0,012 |
1,014 |
|
1,095 |
1,087 |
0,007 |
1,088 |
1,003 |
1,008 |
-0,005 |
1,008 |
|
1,097 |
1,091 |
0,006 |
1,091 |
1,003 |
1,002 |
0,000 |
1,003 |
|
1,092 |
1,094 |
-0,002 |
1,094 |
1,003 |
1,000 |
0,003 |
1,000 |
|
1,098 |
1,097 |
0,001 |
1,097 |
1,003 |
1,000 |
0,003 |
1,000 |
|
1,097 |
1,097 |
-0,001 |
1,098 |
1,003 |
1,001 |
0,001 |
1,002 |
|
1,038 |
1,097 |
-0,059 |
1,097 |
1,003 |
1,002 |
0,000 |
1,003 |
|
1,159 |
1,096 |
0,062 |
1,097 |
1.2 Типовые алгоритмы экстраполяции
1.2.1 Экстраполяция на базе ряда Тейлора
Экстраполированные (прогнозные) значения временного ряда данных определяется на основе разложения его сглаженных значений в какой-либо ряд, например, в ряд Тейлора [9,13], и использование для оценки экстраполированных значений первого; первого, второго; первого, второго, третьего и т.д. членов разложения.
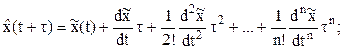 (13)
(13)
где t – непрерывное время;
t – интервал экстраполяции.
Для ряда Тейлора имеем следующие формулы для оценки экстраполированных значений:
1) Экстраполяция нулевого порядка (простая сдвижка)
![]() (i +t) =
(i +t) = ![]() (i);
(14)
(i);
(14)
где i – дискретное время;
t – интервал экстраполяции (прогнозирования); t = 1, 2….
2) Экстраполяция первого порядка:
![]() (i +t) =
(i +t) = ![]() (i) +
(i) + ![]() (i)t.
(15)
(i)t.
(15)
где ![]() (i) – оценка скорости изменения
тренда, которая определяется по формуле:
(i) – оценка скорости изменения
тренда, которая определяется по формуле:
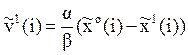 ,
, ![]() .
.
3) Экстраполяция второго порядка:
![]() (t +t) =
(t +t) = ![]() (i) +
(i) + ![]() (i)t +
(i)t +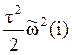 ;
; ![]() (i)= 3
(i)= 3![]() (i) -3
(i) -3![]() (i)+
(i)+ ![]() (i);
(i);
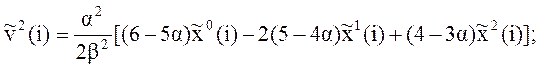
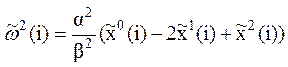 , (16)
, (16)
где ![]() – оценка ускорения изменения тренда.
– оценка ускорения изменения тренда.
Пример экстраполяции нулевого, первого и второго порядка продемонстрирован на рисунке 5 (t = 2).
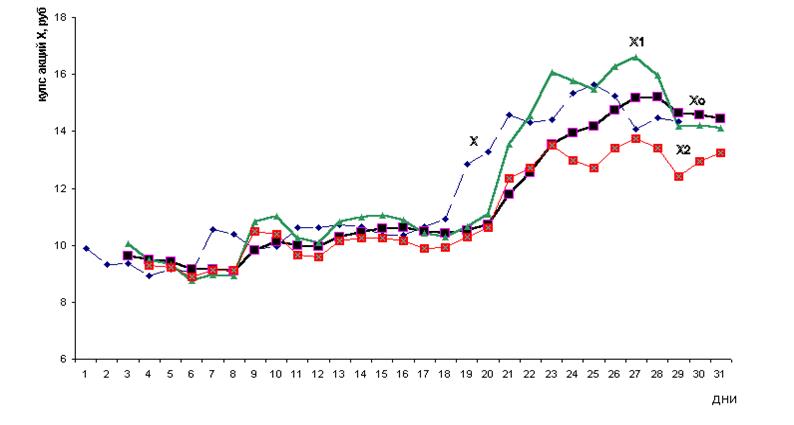 Рисунок 5 – Динамика фактических (Х) и
экстраполированных значений курса акций (для экстраполятора нулевого порядка
Хо, первого порядка Х1, второго порядка Х2).
Рисунок 5 – Динамика фактических (Х) и
экстраполированных значений курса акций (для экстраполятора нулевого порядка
Хо, первого порядка Х1, второго порядка Х2).
1.2.2 Алгоритм Тригга – Лича
Д. Тригг и А.Лич предложили модифицировать предсказывающие блоки, используя экспоненциальное сглаживание (3) посредством изменения скорости реакции в зависимости от значения, так называемого, трекинг-сигнала (контрольного сигнала). В простейшем случае это эквивалентно оперативной коррекции коэффициента сглаживания a(i). Наиболее очевидный способ заставить прогнозатор реагировать на расхождение прогнозов и фактических данных – это увеличение a(i), с тем, чтобы придать больший вес последним отсчетам и тем самым обеспечить приспособление экстраполятора к новой ситуации.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.