Типовые алгоритмы экстраполяционного прогнозирования: Учебно-методическое пособие по дисциплине «Методы и алгоритмы прогнозирования в системах управления», страница 6

Пример расчета (i) согласно (7) приведен на рисунке 4.

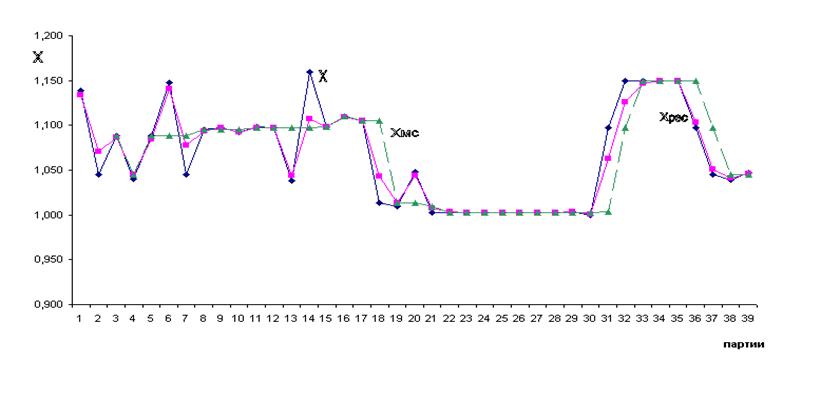        Рисунок 4 - Динамика фактических (Х) и сглаженных

(по алгоритму медианного сглаживания (7) -ХМС и РЭС (8) – ХРЭС) значения коэффициента расхода металла.

Первые 5 шагов расчета с округлением результата до тысячных представлены ниже. В качестве настроечного коэффициента принимаем М = 3.

(3) = med{1,139; 1,045; 1,088} = 1,088;    

(4) = med{1,045; 1,088; 1,040} = 1,045;     

(5) = med{1,088; 1,040; 1,089} = 1,088;   

(6) = med{1,040; 1,089; 1,147} = 1,089;     

(7) = med{1,089; 1,147; 1,044} = 1,089  и т.д.

1.1.5  Алгоритм релейно-экспоненциального сглаживания первого порядка (РЭС-1)

Формульное представление алгоритма РЭС-1 [11,12]:

(i) =(i – 1) +a(i)y[Δ(i)];       Δ(i) = х(i) – (i – 1), i = 1, 2, 3…;

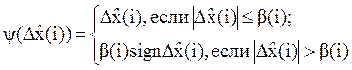
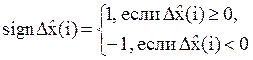                                                                                (8)

sign – знаковая (сигнум) функция.

Оценка начального значения может быть определена арифметическим или медианным осреднением первых М отсчетов в соответствии (7). Настроечный параметр a определяется в соответствии с п.п. 1.1.2. Настроечный параметр b, определяющий свойства защищенности алгоритма от влияния грубых помех, находится из условия [11]:

b(i) = b^*; b^* = || + (2 ¸ 3);

где – среднеквадратичное отклонение обычной (без учета грубых выбросов) помехи с нормальным распределением и нулевым средним определяется из соотношения:

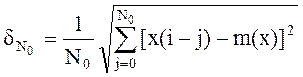,                               (9)

где m(x) – оценка математического ожидания переменной х.

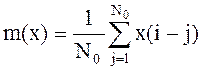.                                     (10)

При этом N₀ выбирается с учетом рекомендаций [12].

|| – модуль максимального приращения сигнала на соседних отсчетах.

max|| = max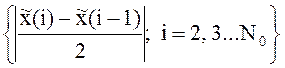.              (11)

Пример реализации алгоритма приведен на рисунке 4. Исходные данные приведены в таблице 2. Начальные сглаженные значения для i = 0,1,2 считаются неизвестными, т.к. (3) определяется как медиана на множестве {х(1), х(2), х(3)}. a = 0,9, b = 0,1 – настроечные коэффициенты.

Первые 6 шагов расчета приводятся в таблице 3.

Таблица 3 – Пример расчета  по алгоритму РЭС-1

1.1.6 Алгоритм медианно-экспоненциального сглаживания первого порядка (МЭС-1)

Формульное представление алгоритма [12]:

(i) = (i – 1) + a(i)Δ(i);     Δ(i) = med{Δх(i), ..., Δx(i – M + 1)};

Δx(i – j) = x(i – j) – (i – j – 1);    j = 0, 1, 2, ..., M                         (12)

Оценка начального значения и настроечный параметр определяется так же, как и для алгоритма РЭС-1 (см. п.п. 1.1.5).

Пример реализации алгоритма: