Типовые алгоритмы экстраполяционного прогнозирования: Учебно-методическое пособие по дисциплине «Методы и алгоритмы прогнозирования в системах управления», страница 4

прогнозирования

Структура экстраполяционного прогнозатора (предиктора) может быть представлена в виде следующей схемы (рис.1):

 

Рисунок 1 – Основные элементы прогнозатора

экстраполяционного типа.

Блок фильтрации (сглаживатель, фильтр) выделяет трендовую составляющую (тенденцию)  исходного ВРД. Подчеркнем, что  в данной схеме соотносится с текущим (i-ым) моментом времени. Эта оценка соответствует режиму фильтрации. Если она соотносится с прошлыми отсчетами (i – 1); (i – 2) …, то она соответствует режиму сглаживания. Если же она соотносится с будущими значениями (i + 1); (i + 2) …, то это соответствует режиму экстраполяции (экстраполяционного прогнозирования), причем последний реализуется в блоке экстраполяции [6]. х = {х(i), i = 1, 2….} – объект прогнозирования  – временной ряд данных. i– дискретные моменты времени (сек, мин, час, сутки и т.д.).  = {(i), i = 1, 2…} – сглаженный ряд данных.  = {(i + t), i = 1, 2…; t = 1, 2…} – оценки прогнозируемых значений ВРД на 1, 2 … , tтакта вперед (временной ряд прогнозируемых значений).

Рассматриваемый подход к прогнозированию и конкретные алгоритмы, приведенные далее, исходят из следующей математической модели прогнозируемого ВРД:

х(i)= , где j(i) – тренд временного ряда данных – регулярная медленно меняющаяся компонента, характеризующая его общую тенденцию;

– флуктуационная случайная помеха с хорошо идентифицируемыми статистическими свойствами;

- эпизодически действующая (импульсная) помеха с трудно идентифицируемыми нестационарными свойствами.

1.1  Типовые алгоритмы фильтрации (сглаживания)

К числу типовых относятся наиболее  часто применяемые относительно простые алгоритмы, эффективность которых достаточна для многих практических случаев.

1.1.1  Алгоритм скользящего среднего

Исходное представление формулы скользящего среднего для шага скольжения равного 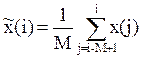1.

                                               (1)

Рекуррентная форма записи:

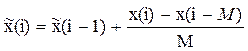                                     (2)

где М – число усредняемых данных (интервал памяти алгоритма).

Оценка скользящего среднего соотносится здесь с i-ым (текущем) отсчетом времени, что соответствует режиму фильтрации.

Пример:

В качестве исходных данных возьмем динамику курса доллара за август 2001 года (таблица 1).

Таблица 1 – Динамика курса доллара (в руб).

Число	1	2	3	4	5	6	7	8	9	10	11	12	13
Курс	29,68	29,68	29,73	29,73	29,73	29,74	29,74	29,74	29,74	29,71	29,71	29,71	29,71
Продолжение таблицы 1
Число	14	15	16	17	18	19	20	21	22	23	24	25	26
Курс	29,72	29,72	29,72	29,78	29,78	29,78	29,8	29,91	29,9	29,9	29,93	29,93	29,93

Первые 5 шагов расчета, выполненные с округлением результата до сотых, представлены ниже.

            

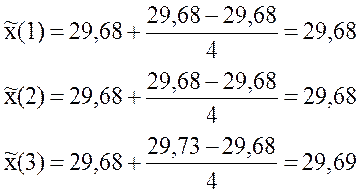
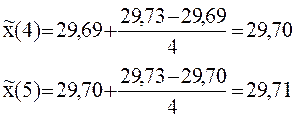
Пример расчета скользящего среднего для М = 4, (0) = х(1), в соответствии с формулой 2 приведен на рисунке 2.

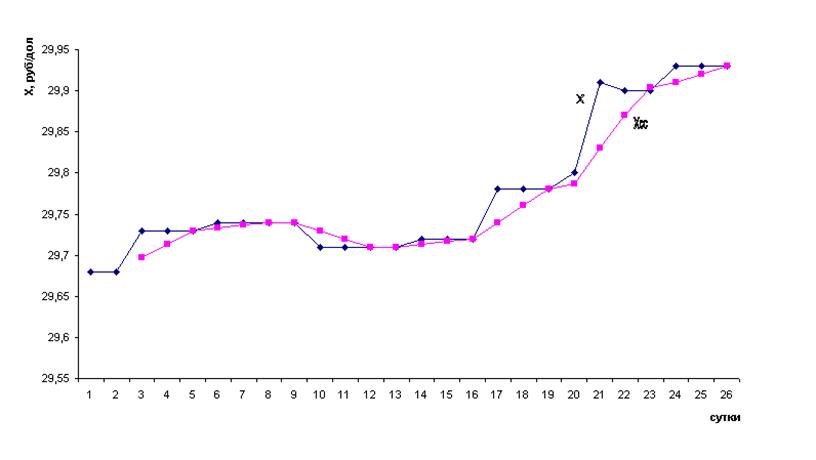Рисунок 2 - Фактические (Х) и сглаженные (Хсс) по скользящему среднему значения курса доллара

1.1.2  Алгоритм экспоненциального сглаживания

I порядка (ЭСI)

Формульное представление алгоритма: [9]

     (i) =(i – 1) + a(i)Δх(i);      Δх(i) = х(i) – (i – 1)                   (3)

Оценка начального значения может, например, определяться осреднением первых М данных по формуле

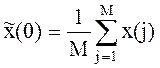                                            (4)

где j – порядковый номер отсчета, a – настроечный коэффициент, который в первом приближении можно определить по формуле:

a =2/(M+1).