Типовые алгоритмы экстраполяционного прогнозирования: Учебно-методическое пособие по дисциплине «Методы и алгоритмы прогнозирования в системах управления», страница 10

Данный метод является одной из попыток применения адаптивного прогнозирования. Метод основан на построении трех одновременных прогнозов по схеме экспоненциально взвешенного среднего с тремя различными коэффициентами экспоненциального сглаживания a. Произвольно выбранные в начальном периоде коэффициенты сглаживания с течением времени меняются по следующему правилу: если по критерию ошибок один из крайних прогнозов (верхний или нижний) станет лучше основного, в следующие моменты времени за основной берется прогноз, соответствующий лучшему крайнему значению. Для нового прогноза берут свои крайние значения коэффициентов. По мнению автора, a основного и крайних прогнозов должны различаться на 0,05 в большую или меньшую сторону, т.е.

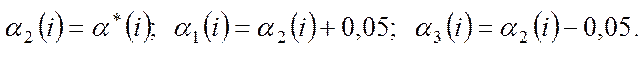
Пример реализации.

Начальное значение х(0) было найдено как med{ х(1), х(2), х(3)}. Коэффициенты a выбраны произвольно и равны соответственно a₁(2) = 0,85; a₂(2) = 0,9; a₃(2) = 0,95. Первые 9 шагов расчета приводятся в таблице 5.

Таблица 5 – Пример прогнозирования с использованием трехструктурного прогнозатора

1.4  Многовариантный алгоритм экспоненциального

сглаживания и экстраполяции

Выделение и прогнозирование трендов динамических рядов данных с использованием экспоненциального сглаживания первого, второго, третьего порядка является широко распространенной процедурой в системах автоматизации учебного, научного и производственного назначения. Что же касается многовариантного прогнозирования, то конкретное множество фильтров экспоненциального сглаживания различного порядка вполне отображается в общую многовариантную структуру с простой разностной рекурсией в пространстве соответствующих им вариантных операторов линейного преобразования динамического ряда данных [16, 17]. Соответствующая схема приведена на рисунке 10.

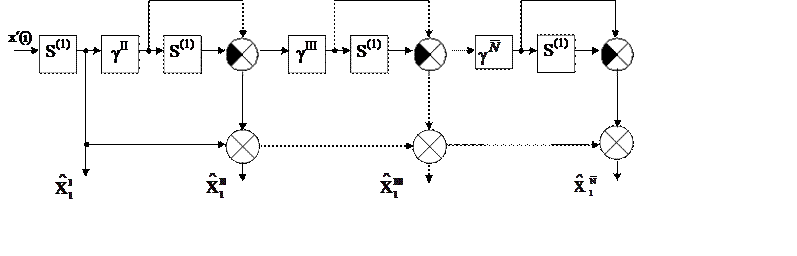
Рисунок 10 – Структурная схема многовариантного прогнозатора х′(i) – исходный однопараметрический ряд данных с целочисленными аргументами i = 0, 1, 2…; S⁽¹⁾  – элементарный оператор сглаживания первого порядка; g^II, g^III, … g^N – настроечные коэффициенты;  , …  – вариантные экстраполированные оценки трендовой составляющей х′(i) с различной степенью аппроксимирующего полинома.

Формульное представление алгоритма имеет вид:

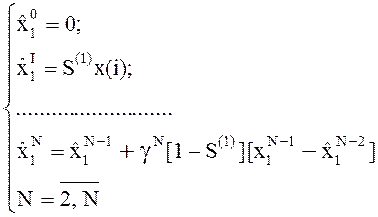                          (38)                                                                         

Настроечные параметры g находятся по формулам

          g^I = 1;  g^II = (1 + t);   g^III = ;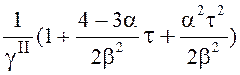   

                    g^IV = 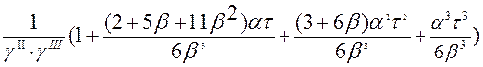     (39)

где a и b – настроечные коэффициенты;

t – целочисленное время экстраполяции.

Рекомендации по выбору a и b были даны в п. 1.1.2.

Вычисление g более высоких порядков является процедурой трудоемкой и используется крайне редко.

1.5  Прогнозирование многомерных случайных процессов

1.5.1  Использованием фильтра Калмана

Пусть многомерный случайный процесс х(t) задан следующей линейной моделью динамической системы

 = F(t)X(t) + G(t)U(t) ,                               (40)

где X(t) – n-мерный вектор, называемый состоянием данной системы, компоненты которого х(i) называют переменными состояния;