Типовые алгоритмы экстраполяционного прогнозирования: Учебно-методическое пособие по дисциплине «Методы и алгоритмы прогнозирования в системах управления», страница 5

М рекомендуется выбирать с учетом требований пользователя к характеру выделяемой тенденции  (тренда) ВРД. Более точное определение a можно осуществить посредством моделирования с перебором возможных дискретных значений a в диапазоне [0; 1] и оценивания значений выбранного критерия оптимальности сглаживания.

Пример расчета.

Исходные данные для расчета представлены в таблице 1.

Расчет производился для a = 0,5 и  (0)=х(1) в соответствии с формулой 3. Первые 5 шагов расчета приведены ниже:

(1) = 29,68 + 0,5(29,68 – 29,68) = 29,68

(2) = 29,68 + 0,5(29,68 – 29,68) = 29,68

(3) = 29,68 + 0,5(29,73 – 29,68) = 29,70

(4) = 29,70 + 0,5(29,73 – 29,70) = 29,71

(5) = 29,71 + 0,5(29,73 – 29,71) = 29,72   и так далее.

Расчет по всей выборке данных приведен на рисунке 3.

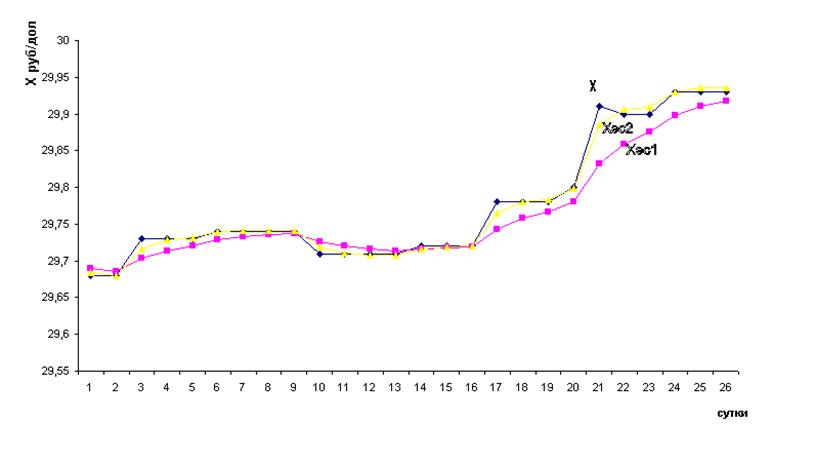 Рисунок 3  - Фактические (Х) и сглаженные ( с помощью ЭС1 – Хэс1 и ЭС2 – Хэс2) значения курса доллара

         1.1.3  Алгоритм экспоненциального сглаживания

                  второго   порядка (ЭС II)

Формульное представление алгоритма [11, 12] имеет вид:

     (i) =(i – 1) + (i – 1) + a₁(i)Δ(i);

= (i – 1) + a₂(i)Δ(i);  Δ(i) = х(i) – (i – 1) – (i – 1);

a₁(i)= [2a(i) – a²(i)];   a₂(i) = a²(i).                                         (5)

Настроечный параметр a(i) может быть постоянным и в этом случае он определяется как в п. 1.1.2. Оценка начального значения (0) определяется из соотношения (4). Оценка начального значения (0) определяется из соотношения:

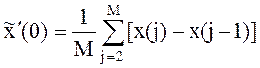 .                                    (6)

Параметр М рекомендуется выбирать в зависимости от желаемой степени сглаживания ряда: М увеличивается при сильном сглаживании и наоборот.

Пример реализации алгоритма.

Исходные данные представлены в таблице 1.

Определим  настроечные параметры a₁ и a₂. Параметр a определим по формуле из п. 1.1.2. (a = 0,5), тогда a₁ = [2·0,5 – 0,5²]= 0,75,     a₂(i) = 0,5² = 0,25.

Принимаем (0) = х(1); (0) = 0, так как на начальном этапе наблюдения курс доллара меняется незначительно.

Ниже приведены первые 5 шагов расчета.

(1) = 0 + 0,25(29,68 – 29,68 – 0) = 0

(1) = 29,68 + 0 + 0,75(29,68 – 29,68 – 0) = 29,68

(2) = 0 + 0,25(29,68 – 29,68 – 0) = 0

(2) = 29,68 + 0 + 0,75(29,68 – 29,68 – 0) = 29,68

(3) = 0 + 0,25(29,73 – 29,68 – 0) = 0,01

(3) = 29,68 + 0 + 0,75(29,73 – 29,68 – 0) = 29,71

(4) = 0,01 + 0,25(29,73 – 29,71 – 0,01) = 0,01

(4) = 29,71 + 0,01 + 0,75(29,73 – 29,71 – 0,01) = 29,72

(5) = 0,01 + 0,25(29,73 – 29,72 – 0,01) = 0,011

(5) = 29,72 + 0,01 + 0,75(29,73 – 29,71 – 0,01) = 29,73 и так далее Расчет по всей выборке данных представлен на рисунке 3.

                 1.1.4  Алгоритм скользящей медианы

Формульное представление алгоритма [11,12]:

_med(i) = med{х(i – (M – 1)),   x(i – (M – 2)), ..., x(i)}                     (7)

где med {····} – операция оценивания скользящей медианы, которая включает следующие действия: - произвести упорядочивание отсчетов х(i–(M–1)), …., х(i) по возрастанию или убыванию их значений, то есть выстроить вариационный ряд; - при нечетном М выбрать центральное (срединное) значение из упорядоченной последовательности, которое соотнести с _med(i); - при четном М определить полусумму из двух срединных членов вариационного ряда, которую соотнести с _med(i). В данном случае используется одноступенчатое (сразу по всем отсчетам) оценивание медианы. В некоторых случаях, например, при объеме выборки в 20 и более отсчетов, используют многоступенчатое оценивание медианы, когда выборка данных разбивается на подвыборки, а оценивание медианы проводят сначала для каждой подвыборки, а затем на множестве  полученных оценок медианы.

Пример реализации алгоритма.

Исходные данные приведены в таблице 2.

Таблица 2 – Динамика расходного коэффициента, тонна/тонна