Экономика и менеджмент \ Методы и алгоритмы прогнозирования в системах управления

Типовые алгоритмы экстраполяционного прогнозирования: Учебно-методическое пособие по дисциплине «Методы и алгоритмы прогнозирования в системах управления», страница 12

Q(X, Y) ® exctr Þ (i = 1, k),   Y Î W(Xi)                        (50)                                        где W(Xi) – область применения параметров Y объекта, зависящая в общем случае от ситуации Xi.

Ставится задача нахождения (без проведения трудоемких процедур) вектора Yk+1, близкого в определенном смысле к вектору , оптимальному в новой заданной ситуации Хk+1.

Пусть функция Y* = F(X) обозначает неизвестную зависимость оптимальных параметров системы от ситуации. Задача сводится к восстановлению неизвестной векторной функции F векторного аргумента Х по конечному числу значений аргумента Х и соответствующих ему значений вектора Y*.

Множество векторов возможных ситуаций обозначим через {Х}, а соответствующее множество векторов решений Y как {Y}.

Выбор способа решения задачи зависит от количества имеющейся информации: если число наблюдений k достаточно велико в сравнении с размерностью n вектора ситуаций, то можно применять метод наименьших квадратов, если k соизмеримо с n, то можно построить линейную модель функции Y* = F(X).

Рассмотрим случай, когда число наблюдений k < n + 1, где n – размерность вектора X.

Для решения задачи:

- построим линейную модель функции Y* = L(X) на подпространствах {X¢} и {Y¢}, образованных наблюдениями Xi = , i = 1, k;

- введем дополнительную гипотезу для доопределения функции на подпространствах {X} и {Y}.

Уравнения для элементов векторных подпространств имеют вид:

{X¢} = X1 + 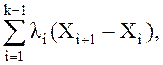    {Y¢} = Y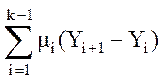1 +          (51)

Для построения линейной модели функции на подпространствах {X¢} и {Y¢} введем следующие гипотезы:

Гипотеза 1. Преобразование X¢ ® Y¢ линейно, тогда следует положить li  = m; i = 1, k = 1. Теперь задача восстановления функции сводится к определению оператора преобразования {X} ® {Y} на основе принятой гипотезы о линейности преобразования {X¢} ® {Y¢}. При k < n + 1 задача имеет бесчисленное множество решений. Эта неоднозначность устраняется введением дополнительной гипотезы.

Предварительно введем некоторую строго выпуклую скалярную функцию, которую назовем функцией близости

Ф = Ф(Х, Х¢) ,    Х Î {X}, Х¢ Î {Х¢}                                    (52)

Каждой паре ситуации Х и Х¢ эта функция ставит в соответствие число, характеризующее удаленность (близость) одной ситуации от другой.

Гипотеза 2. Каждому вектору Х Î {X} ставится в соответствие такой вектор Х¢ Î {Х¢}, который обеспечивает минимум функции близости Ф.

Параметры li, определяющий вектор Х¢ Î {Х¢}, ближайший в соответствии с функцией Ф = Ф(Х, Х¢) можно найти из уравнений

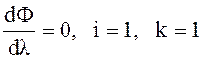.                                       (53)

Алгоритм восстановления функции Y* = F(X):

- преобразуем {Х} в {Х¢} с помощью гипотезы 2;

- отображаем {Х} ® {Y¢} с помощью гипотезы 1;

- отождествляем {Y¢} º {Y}.

Сокращенная запись алгоритма

{Х} → {Х¢} → {Y¢} º {Y}.                                   (54)

Метод МЛЭ позволяет достаточно надежно решать задачу восстановления функции в условиях информационной недостаточности в пространствах малой размерности. С ростом размерности пространства растут вычислительные трудности, связанные с хранением больших массивов информации в памяти ЭВМ.

Применение принципа линейности означает, что мы предполагаем существование линейной зависимости выходных характеристик (эффективности, стоимости, массы и т.д.) сложной системы от управляемых технических параметров. Как правило, эти зависимости в широком диапазоне фазовых координат являются существенно нелинейными, но в определенной области параметров можно выделить квазилинейную часть, и тогда принцип линейности окажется справедливым и полезным.

Принцип компактности предполагает, что новые ситуации как-то примыкают к ранее изученным. Этот принцип позволяет отобразить новую ситуацию на известное подпространство ситуаций с минимальной погрешностью, найти технический параметр, соответствующий новой ситуации.

Погрешность метода экстраполяции оптимальных решений зависит от близости новых ситуаций к подпространству ранее изученных ситуаций. Рассмотренный метод применим для восстановления линейной функции в случае малого числа наблюдений. Если восстанавливаемая функция нелинейная, метод можно применить при любом числе наблюдений. В этом случае значение функции в новой ситуации определяется не по всем имеющимся наблюдениям, а лишь по ближайшим к новой ситуации. В результате осуществляется локально-линейное приближение нелинейной функции.

Скачать файл