Контрольный сигнал определяется по формуле:
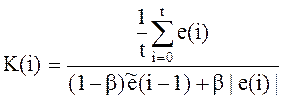 , (17)
, (17)
где К – следящий контрольный сигнал; е(i) – оценка ошибки прогнозирования;
b = 1 – a; 0 < a < 1.
Формульное представление алгоритма [14]:
![]() .
(18)
.
(18)
![]() – оценка трендового значения
прогнозируемой переменной x(i);
– оценка трендового значения
прогнозируемой переменной x(i); ![]() (i) –
текущая оценка трендового значения прогнозируемой переменной;
(i) –
текущая оценка трендового значения прогнозируемой переменной; ![]() – оценка скорости изменения периода; t – шаг экстраполяции, например, t = 1.
– оценка скорости изменения периода; t – шаг экстраполяции, например, t = 1.
Пример реализации алгоритма Тригга – Лича представлен на рисунке 6.
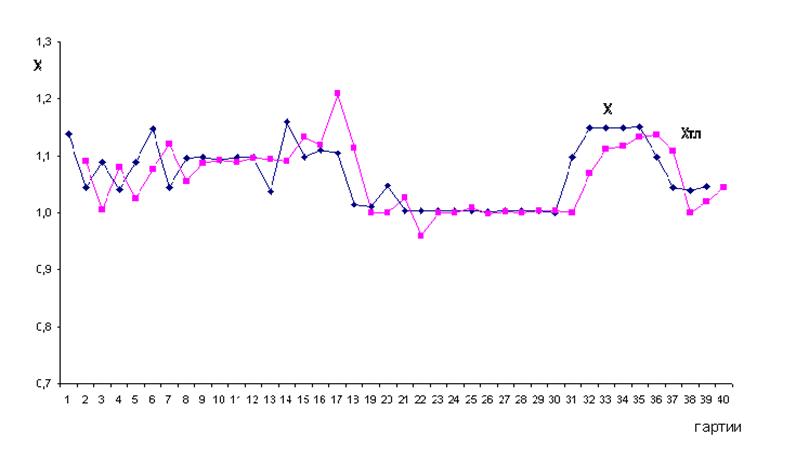 Рисунок 6 - Изменение фактических (Х) и
прогнозных ХТЛ (по алгоритму Тригга- Лича) значений коэффициента
расхода
Рисунок 6 - Изменение фактических (Х) и
прогнозных ХТЛ (по алгоритму Тригга- Лича) значений коэффициента
расхода
металла
1.2.3 Алгоритмы экстраполяции на базе многократного
экспоненциального сглаживания
Для достаточно сложных временных рядов была предложена модель прогнозатора, включающая некоторое число полиномиальных членов. Оценка полиномиальных коэффициентов производится путем многократного сглаживания, то есть сглаженное значение n-го порядка является в свою очередь результатом экспоненциального сглаживания (n-1)-го порядка. При задании исходных условий коэффициенты полинома разложения могут быть получены, например, методом наименьших квадратов.
На практике используются сглаживающие полиномы не выше второго порядка, потому что дальнейшее повышение порядка полинома ведет к быстрому увеличению сложности расчетов и не всегда улучшает точность прогнозирования.
В рассмотренных ниже формулах предполагается, что тренд может быть представлен полиномом и наблюдается при наличии шума, т.е.
![]()
а) Полиномиальная модель нулевого порядка [13].
j(i) = а1 . (19)
Экспоненциальное среднее
S![]() (i) = ax(i) – bS
(i) = ax(i) – bS![]() (i –
1). (20)
(i –
1). (20)
Начальное условие:
S(0) = ![]() .
(21)
.
(21)
Оценка коэффициентов:
![]() = S
= S![]() (i) .
(22)
(i) .
(22)
Прогноз (посредством простой сдвижки)
![]() = S
= S![]() (i); t = 1, 2
…. (23)
(i); t = 1, 2
…. (23)
б) Полиномиальная модель первого порядка.
j(i) = а1 + а2i . (24)
Экспоненциальные средние
S![]() (i) = ax(i) + bS
(i) = ax(i) + bS![]() (i –
1);
(i –
1);
S![]() (i) = aS(i) + bS
(i) = aS(i) + bS![]() (i –
1). (25)
(i –
1). (25)
Начальные условия:
S![]() (0) =
(0) = 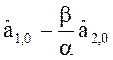 ; S
; S![]() (0) =
(0) = 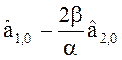 . (26)
. (26)
Оценки коэффициентов:
![]() =2S
=2S![]() (i) – S
(i) – S![]() (i);
(i); 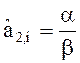 [S
[S![]() (i) – S
(i) – S![]() (i)]. (27)
(i)]. (27)
Прогноз:
![]() =
= ![]() +
+ ![]() =
= 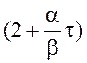 S
S![]() (i) –
(i) – 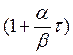 S
S![]() (i). (28)
(i). (28)
в) Полиномиальная модель второго порядка.
j(i) = а1 + а2i + ![]() .
(29)
.
(29)
Экспоненциальные средние
S![]() (i) = ax(i) + bS
(i) = ax(i) + bS![]() (i – 1); S
(i – 1); S![]() (i) = aS
(i) = aS![]() (i) + bS
(i) + bS![]() (i – 1);
(i – 1);
S![]() (i) = aS
(i) = aS![]() (i) + bS
(i) + bS![]() (i –
1). (30)
(i –
1). (30)
Начальные условия:
S![]() (0) =
(0) = 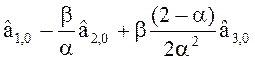 ; S
; S![]() (0) =
(0) = 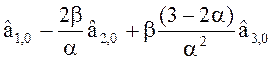 ;
;
S![]() (0) =
(0) = 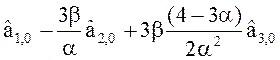 . (31)
. (31)
Оценки коэффициентов:
![]() = 3S
= 3S![]() (i) – 3S
(i) – 3S![]() (i) + S
(i) + S![]() (i); (32)
(i); (32)
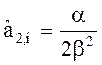 [(5 –
5a)S
[(5 –
5a)S![]() (i) –
2(5 – 4a)S
(i) –
2(5 – 4a)S![]() (i) + (4
– 3a) S
(i) + (4
– 3a) S![]() (i)];
(33)
(i)];
(33)
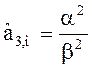 [S
[S![]() (i) – 2S
(i) – 2S![]() (i) + S
(i) + S![]() (i)].
(34)
(i)].
(34)
Прогноз
![]() =
= ![]() +
+ ![]() +
+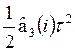 = [6b2 + (6 – 5a)at + a2t2]
= [6b2 + (6 – 5a)at + a2t2]![]() - [6b2+ +
2(5 – 4a)at + 2a2t2]
- [6b2+ +
2(5 – 4a)at + 2a2t2]![]() +[2b2 + (4 – 3a)at + a2t2]
+[2b2 + (4 – 3a)at + a2t2]![]() . (35)
. (35)
Пример реализации алгоритма прогнозирования на базе многократного экспоненциального сглаживания представлен на рисунке 7.
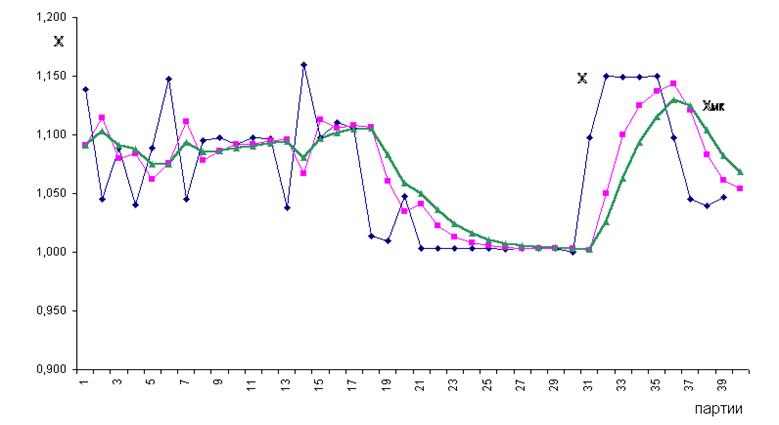 Рисунок 7 – Динамика фактических (Х) и прогнозных ХМК
Рисунок 7 – Динамика фактических (Х) и прогнозных ХМК
(по алгоритму многократного сглаживания) значений
коэффициента расхода металла
1.2.4 Алгоритм Бокса – Дженкинса
Формульное представление алгоритма [14] имеет вид:
![]() ;
; 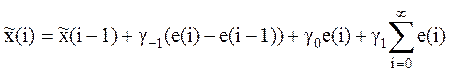 (36)
(36)
где e(i) – ошибка прогнозирования;
g–1, g0, g1 – настроечные коэффициенты.
Пример реализации алгоритма Бокса – Дженкинса приведен на рисунке 8. Настроечные коэффициенты имеют следующие значения: g–1 = 0,2; g0 = 0,5; g1 = 0,001.
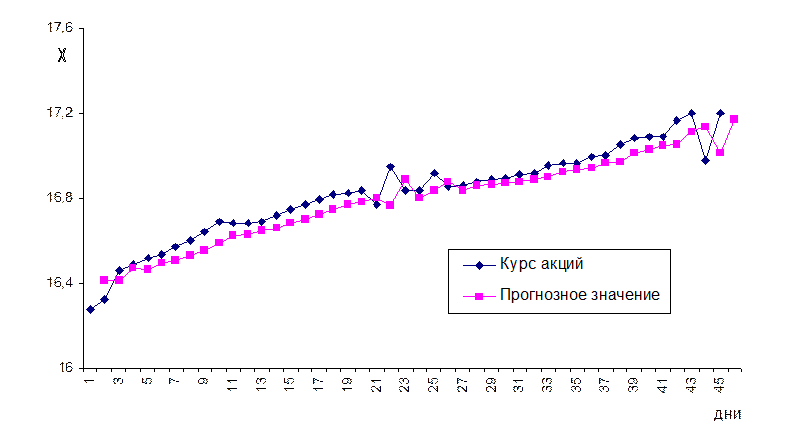 Рисунок 8 – Фактические и прогнозные (по методу
Бокса-
Рисунок 8 – Фактические и прогнозные (по методу
Бокса-
Дженкинса) значения курса акций в динамике
1.2.5 Алгоритм прогнозирования на основе авторегрессии
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.