Типовые алгоритмы экстраполяционного прогнозирования: Учебно-методическое пособие по дисциплине «Методы и алгоритмы прогнозирования в системах управления», страница 11

U(t) – m-мерный вектор входного сигнала;

F(t) – матрица размером (n´m), характеризующая реакцию   на входной сигнал.

Пусть мы можем наблюдать процесс (рис.10):

Z(t) = H(t)X(t) + N(t),                                        (41)

где Z(t) – n-мерный вектор наблюдений;

N(t) – n-мерный вектор стационарных помехи;

Н(t) – матрица размером (р´n), характеризующая ограничения, накладываемые на наблюдения за состоянием системы.

 

Рисунок 11 – Схема динамической системы

Пусть наблюдения за процессом измерения процесса z(t) начинаются в некоторый момент времени t(0). При этом ковариационная матрица   cov{x[t(0)]X[t(0)]} предполагается известной.

Калман показал, что дифференциальное уравнение оптимального фильтра, возбуждаемого наблюдаемым сигналом и вырабатывающим наилучшую оценку выходного сигнала имеет вид:

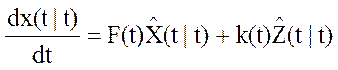,                            (42)

где ;

k(t) – матричный коэффициент усиления;

 – оптимальная оценка случайного процесса x(t) в момент времени t, полученную по наблюдениям случайного процесса (t) до момента t включительно.

Начальное состояние системы (40) находится в нуле = 0.

Оптимальная оценка значения Х в точке t+Δt (оптимальное прогнозирование) определяется по выражению:

      при Δt ³ 0.                          (43)

где Ф – переходная матрица системы (38), которая является невырожденной и удовлетворяет дифференциальному уравнению:

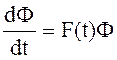.                                               (44)

Оптимальный фильтр представляет собой систему с обратной связью. Для определения оптимального фильтра найдем матричный коэффициент условия k(t) через корректирующую матрицу ошибки. Запишем ошибку фильтрации в виде:

 .                                        (45)

Обозначим ковариационную матрицу ошибки фильтрации через

P(t) = cov[,] .                                   (46)

Тогда матричный коэффициент усиления можно записать в виде:

k(t) = P(t)H^–T(t)R^–1(t) ,                                       (47)

где R – симметричная неотрицательная определенная матрица.

При этом матрица R предполагается положительно определенной для всех t, что означает, что помеха N(t) при наблюдении за процессом Х(t) присутствуют всегда.

Матрица Р(t) в свою очередь определяется из матричного дифференциального уравнения, называемого корреляционным.

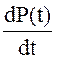 = F(t)P(t)F^T(t) – P(t)H^T(t)R^–1(t) + C(t)Q(t)C^T(t)              (48)                   где Q(t) – симметричная неотрицательная положительно определенная матрица.

Это уравнение представляет собой систему 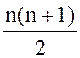 нелинейных дифференциальных уравнений первого порядка.

Таким образом, задача оптимального прогнозирования нелинейных процессов состоит из задачи фильтрации, т.е. определения оптимальной оценки X(t | t), которая сводится к задаче решения корреляционного уравнения (46) и последующей экстраполяции с помощью выражения (41). Более подробно о применении фильтра Калмана смотри [13].

1.5.2  Алгоритм многомерной линейной экстраполяции

1.5.2.1  Краткая характеристика алгоритма [18]

Пусть требуется оценить параметры системы, соответствующие наилучшему значению критерия качества в заданной ситуации. Под ситуацией можно, например, понимать условия работы системы, ограничения на отдельные ее характеристики и т.д. Если ситуация соотносится с будущим временем, то мы имеем дело с прогнозирующим оцениванием.

Зависимость оптимальных параметров системы от ситуации, как правило, бывает неизвестной, и определение её требует трудоемкой процедуры расчетов. Рассмотрим решение этой задачи методом многомерной линейной экстраполяции (МЛЭ).

Пусть критерий качества системы определяется скалярной функцией двух векторных аргументов X и Y

Q = Q(X, Y) ,                                         (49)

где Y  = (у₁, у₂, у₃, …, у_m) – вектор оптимизируемых параметров объекта;

Х  = (х₁, х₂, х₃, …, х_n) – вектор ситуации, определяющий изменяющуюся специфику объекта и его среды, которую следует учитывать при оптимизации.

Для небольшого числа ситуаций Х_i (i = 1, k) известны значения векторов оптимальных решений , (i = 1, k), обеспечивающих наилучшее значение критерия качества, т.е. предполагается решенной  k раз оптимизационная задача: