Управление эксплуатационной работой на участковых станциях (Глава 7 учебного пособия по курсу «Управление эксплуатационной работой железных дорог и качеством перевозок»), страница 10

Конкретные значения элементов матрицы могут быть рассчитаны при известных распределениях вхоящего потока и времени его обслуживания. Так, например, нередко имеет место распределение входящего потока и времени обслуживания по закону Эрланга, плотность которого выражается

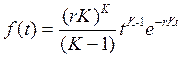, а функция распределения имеет вид

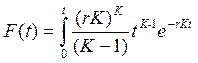,                                          (7.2)

где К – параметр распределения; (отношение квадрата математического ожидания случайной величины  к дисперсии этой величины).

Функция     распределения (7.2) принимает вид:

 при K=1;

 при K=2;

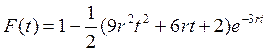 при K=3;

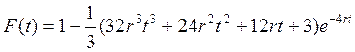 при K=4;

Элементы матрицы состояний приемо - отправочного парка при эрланговском распределении входящего потока и эрланговском времени обслуживания рассчитываются по формуле

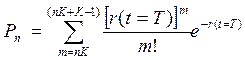,                                (7.3)

где T – период времени, в течение которого в систему поступает п поездов.

Так,   например,   при   интенсивности входящего потока r= 2 поезда в час, параметре К = 2 вероятность того, что в систему поступит в течение периода Т= 1,5 ч не более трех поездов (0, 1, 2, 3), по формуле (7.3) составит сумму Р_о + Р₁ + :

;

;

;

.

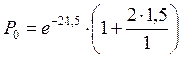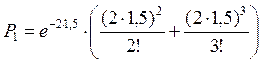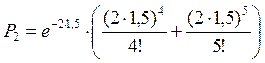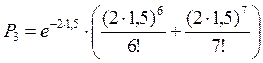Сумма этих вероятностей составит 0,744, т.е. из каждой тысячи периодов по 1,5 ч в 744 случаях в систему будет поступать не более трех поездов при средней интенсивности прибытия 2 поезда в час. При управлении процессами в приемо - отправочных парках необходимо в периодах сгущенного поступления поездов (период Т₂ на рис. 7.11) организовать их интенсивную обработку и отправление. В этом периоде, однако, интенсивность поступления поездов больше интенсивности их обслуживания и отправления , в связи с чем с каждым поездом идет приращение простоя на  величину 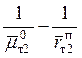. Например, при  поезда в час и при  поездов в час с каждым последующим поездом простой в парке   будет  прирастать  на  величину

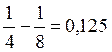ч.      Если      сгущение поступления поездов происходит в течение периода Т₂ при интенсивности , то дополнительный простой, ч, увеличиваясь с каждым прибывающим поездом, для последнего из числа сгущенного поступления поездов составит

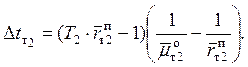                                     (7.4)

Так, например, для принятых значений  поезда в час и поездов в час и при периоде Т₂ = 2 ч дополнительный простой для шестнадцатого поезда, прибывшего в сгущенной пачке, составит  

Максимально допустимый простой на путях приемо - отправочного парка составит 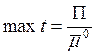, где П – расчетное число путей в парке.

Например, при П = 8,  max t= 2 ч.

При сгущенном подводе поездов, чтобы не допускать их задержки при подходах, необходимо выполнение условия

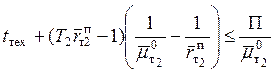,                           (7.5)

где t_тех – время технологического обслуживания поезда на приемо - отправочных путях.

Так, для условий предыдущего примера при t_тех = 0,5 ч и П = 8 условие (7.5) не будет выполнено, так как    0,5 +1,875 = 2,375 ч >  = 2 ч. Разность составляет 0,375 ч. Поскольку с каждым поездом простой в рассматриваемом примере возрастает на 0,125 ч, то число задержанных на подходе поездов составит 0,375:0,125 = 3 поезда, первый из которых будет ожидать приема на станцию 0,125 ч; второй – 0,25 ч; третий – 0,375 ч.

В процессе управления работой станции при вынужденном сгущенном поступлении поездов в течение периода Т₂ необходимо предусматривать меры более интенсивной обработки и отправления поездов и не допускать длительной работы парка в стационарном режиме (период Т₃ на рис. 7.11) с резко увеличенными простоями поездов.

У оперативного персонала – диспетчеров на прилегающих участках и дежурных по станциям нет достаточного времени и исходной информации анализировать выполнение условий (7.4), (7.5) и режимов работы парка. При создании автоматизированных диспетчерских центров, когда исходная информация о координатах и времени передвижения и простоя поездов снимается автоматически с электрических рельсовых цепей, эти условия вместе с выработкой рекомендаций могут рассчитываться ЭВМ АРМ диспетчеров и ЭВМ АРМ дежурных по станциям в прогнозном режиме.