










1.6 Элементы теории массового обслуживания
1.6.1 Понятие о системах массового обслуживания. Предмет теории массового обслуживания
Системы, для которых характерно поступление (через случайные промежутки времени) некоторых требований (как правило, однородных) и их обслуживание (в течение случайного промежутка времени), называются системами массового обслуживания (СМО). Примерами СМО являются билетные кассы, справочные службы, железнодорожные сортировочные станции, ремонтные мастерские, АТС, вычислительные сети, сети передачи данных, Internet-ресурсы и т.д. Для каждой СМО характерно наличие входящего потока требований, очереди (в которой требования ожидают своего обслуживания) и обслуживающего устройства, состоящего из одного или нескольких обслуживающих приборов (каналов) (рисунок 51).
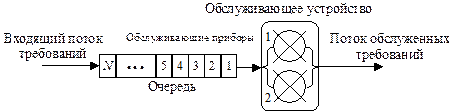
Рисунок 51 – Схематическое изображение системы массового обслуживания
Предметом теории массового обслуживания является определение характеристик СМО (среднее количество требований в очереди, среднее время ожидания заявками обслуживания, коэффициент загрузки приборов, среднее время нахождения требований в СМО, вероятность отказа в обслуживании и т.д.) с целью оптимизации работы системы. Так, например, методы теории массового обслуживания помогают ответить на вопросы:
· каким должно быть путевое развитие приемоотправочного парка, чтобы обеспечивать эффективную работу железнодорожной сортировочной станции;
· каким должно быть число операторов пейджинговой службы, чтобы при заданном потоке заявок и характеристиках сообщений обеспечить (с определенной вероятностью) безотказную работу службы;
· каковы должны быть характеристики сервера вуза, чтобы обеспечить нормальную работу рабочих станций локальной вычислительной сети.
Все существующие СМО классифицируются по следующим признакам:
В зависимости от количества мест в очереди СМО подразделяются на системы:
· с потерями: требования, которые застают все обслуживающие приборы занятыми, теряются или покидают СМО не обслуженными (N = 0). Примером подобных СМО являются АТС, которые могут одновременно организовывать соединение ограниченного числа абонентов, дополнительные требования абонентов не могут быть обслужены и получают отказ;
· ограниченным числом N мест ожидания: если требование, поступающее в систему, застает очередь из N заявок, то оно теряется (остается не обслуженным). Примером данных СМО являются железнодорожные сортировочные станции, где число мест ожидания определяется числом и длиной путей парка приема;
· ожиданием: число мест в очереди не ограничено (N = ¥). Примером указанных СМО являются билетные кассы, ремонтные мастерские.
В зависимости от дисциплины обслуживания, определяющей порядок выбора из очереди требований на обслуживание, СМО бывают следующих типов:
· первым пришел – первым обслужен (FIFO: first in – first out): требования обслуживаются в порядке поступления. Данная дисциплина обслуживания применяется, например, в билетных кассах;
· последним пришел – первым обслужен (LIFO: last in – first out): инверсионный порядок обслуживания, при котором в первую очередь обслуживается требование, поступившее последним. Подобным образом организована работа со стеком команд микропроцессора;
· разделение процессора: прибор обслуживает все требования, находящиеся в очереди, последовательно предоставляя им квант своего времени. Примером подобной дисциплины обслуживания является организация многозадачных операционных систем, когда микропроцессор (способный одновременно выполнять лишь одну программу) уделяет часть своего времени для «параллельной» работы каждой из нескольких загруженных программ;
· случайный выбор: очередная заявка выбирается (для обслуживания) из очереди случайным образом;
· обслуживание с приоритетами, когда некоторые требования имеют более высокий приоритет по сравнению с другими. Они обслуживаются в первую очередь, например, срочные заказы в химчистке. В некоторых случаях поступление приоритетного требования может прервать обслуживание заявки, уже находящейся в обслуживающем приборе.
В зависимости от числа приборов обслуживающего устройства СМО бывают:
· одноканальными (n = 1), например, сортировочная горка железнодорожной станции;
· многоканальными. Примерами многоканальных СМО является работа Internet-провайдеров, АТС, а также пейджинговых служб, которые предоставляют услуги одновременно n клиентам.
Для простейших СМО принято следующее символическое обозначение (символика Кендалла):
A / B / n / N , где буква A характеризует входящий поток требований (A = G, если входящий поток рекуррентный; A = M, если входящий поток простейший; A = D, если входящий поток регулярный); буква B характеризует время обслуживания требований (B = G, если время обслуживания всех требований имеет одинаковый закон распределения; B = M, если время обслуживания всех требований имеет показательный закон распределения; B = R, если время обслуживания требований имеет равномерный закон распределения; B = D, если время обслуживания всех требований – константа); n – число приборов (каналов) обслуживающего устройства (см. рисунок 51), n ³ 1; N – число мест для ожидания заявками обслуживания (максимально возможная длина очереди), N ³ 0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.