Содержание
1. Задача на Марковские системы обслуживания …………………………………………….3
2. Задача расчета потребной складской площади методами теории массового обслуживания ……………………………………………………………………………………………..4
3. Задача на определение переходного и стационарного режимов для СМО с дискретным состоянием и непрерывным временем.………………………………………………………………….6
4. Задача оценки надёжности не восстанавливаемых изделий по статическим данным …………...8
5. Задачапрогнозирования надёжности невосстанавливаемого изделия…………………...10
6. Задача определения готовности отправления поездов по графику……………………….12
7. Задача выбора технических решений в условиях неопределённости и риска…………...13
Задача №1
Задача на Марковские системы обслуживания
Дано: Составы, поступающие в парк прибытия (ПП) станции, подвергаются там техническому осмотру. Параллельно работают 2 бригады. Среднее время осмотра состава бригадой равно 20 минут. Предполагается, что поток поступающих в парк составов пуассоновский с интенсивностью 3 поезда/ч, а время осмотра бригадой состава имеет показательное распределение. Определить вероятность того, что хотя бы одна из бригад простаивает. Технический процесс считать стационарным, количество путей в ПП достаточно большим.
Решение: Парк прибытия является марковской системой М/М/2.
Интенсивность входящего потока ![]() поезда/ч,
а интенсивность обслуживания
поезда/ч,
а интенсивность обслуживания ![]() поезда/ч (при работе
одной бригады).
поезда/ч (при работе
одной бригады).
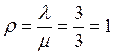 .
.
Система эргодична.
Найдем стационарные вероятности занятости приборов обслуживания:
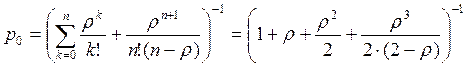 ,
,
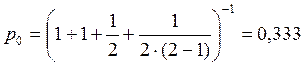 ;
;
![]() .
.
Вывод: следовательно, вероятность простоя хотя бы одной бригады составляет 0,333.
Задача №2
Задача расчета потребной складской площади методами теории массового обслуживания
Дано:
На склад краткосрочного хранения (СКХ) в течение года поступает ![]() грузов. Склад работает круглосуточно весь
год. Средняя масса груза в одной поступающей партии
грузов. Склад работает круглосуточно весь
год. Средняя масса груза в одной поступающей партии![]() .
Расчетная погрузка на
.
Расчетная погрузка на ![]() площади склада
площади склада ![]() . Грузы поступают на хранение в склад
неравномерно, т.е. моменты их прибытия имеют вероятностный характер. Входящий
поток партии грузов является простейшим. Математическое ожидание длительности
хранения различных партий грузов на складе составляет
. Грузы поступают на хранение в склад
неравномерно, т.е. моменты их прибытия имеют вероятностный характер. Входящий
поток партии грузов является простейшим. Математическое ожидание длительности
хранения различных партий грузов на складе составляет ![]() при
показательном законе распределения длительности хранения. Требуется определить
потребную полезную складскую площадь склада
при
показательном законе распределения длительности хранения. Требуется определить
потребную полезную складскую площадь склада ![]() ,
обеспечив пропуск заданного грузооборота
,
обеспечив пропуск заданного грузооборота ![]() при
вероятности отказа
при
вероятности отказа ![]() .
.
Решение:
1) Среднесуточные поступления на склад отдельных партий грузов равно:
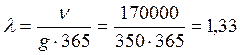 .
.
2) Интенсивность обслуживания партий грузов равна обратному значению среднего срока обслуживания, то есть:
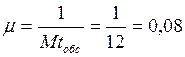 .
.
3) Вероятность отказа при заданном грузообороте и имеющемся числе ячеек составит:
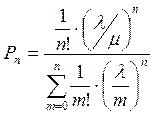 , где
, где ![]() – расчетное число условных ячеек хранения
на складе;
– расчетное число условных ячеек хранения
на складе;
![]() – число одновременно занятых
ячеек склада.
– число одновременно занятых
ячеек склада.
Расчетное число ячеек определяется из условия:
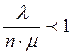 ;
; 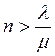 .
.
Таким образом, минимальное расчетное число ячеек равняется целой части
отношения ![]() .
.
Следовательно:
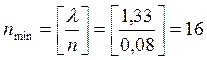 .
.
Тогда вероятность отказа при 16 ячейках на СКХ определяем по формуле:
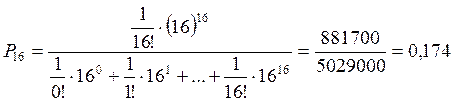 .
.
4) Поскольку значение вероятности отказа не может превышать 1, то фактическая пропускная способность склада за год при данном числе ячеек составляет:
![]() .
.
5) Полезная площадь склада F при заданном размере ячейки:
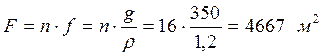 .
.
Т.к. полученная вероятность отказа больше заданной по условию задачи (0,175>0,04-0,05), то увеличивается число ячеек, и все расчёты производятся аналогично для нового числа ячеек до тех пор, пока вероятность отказа не будет удовлетворять заданной. Полученные значения сводятся в таблицу 1.
Таблица 2.1 – Определение полезной площади склада
|
Число ячеек, |
Вероятность
отказа, |
Пропускная
способность, |
Полезная
площадь, |
|
16 |
0,175 |
140198 |
4667 |
|
17 |
0,141 |
146077 |
4958 |
|
18 |
0,111 |
151132 |
5250 |
|
19 |
0,085 |
155496 |
5542 |
|
20 |
0,064 |
159157 |
5833 |
|
21 |
0,046 |
162137 |
6125 |
|
22 |
0,033 |
164477 |
6417 |
Вывод:
При 21 ячейки склад обеспечивает пропуск заданного грузооборота с вероятностью
отказа 0,046. За год склад может не принять 7863 тонны груза. Полезная площадь
в этом случае составит ![]() .
.
Задача №3
Задача на определение переходного и стационарного режимов для СМО с дискретным состоянием и непрерывным временем
Требуется:
1) Постановка задачи;
2) Решить задачу методом Рунге-Кутта;
3) Вывод.
1. Постановка задачи:
В автохозяйстве имеется ![]() автомашин, каждая из
которых, независимо от других, может выйти из строя. Интенсивность простейшего
потока отказа автомашины равна
автомашин, каждая из
которых, независимо от других, может выйти из строя. Интенсивность простейшего
потока отказа автомашины равна ![]() . Отказавшая автомашина,
становиться на стоянку и ожидает ремонта. Время ожидания начала ремонта
автомашины распределено по показательному закону с параметром
. Отказавшая автомашина,
становиться на стоянку и ожидает ремонта. Время ожидания начала ремонта
автомашины распределено по показательному закону с параметром ![]() . Время ремонта автомашины распределено по
показательному закону с параметром
. Время ремонта автомашины распределено по
показательному закону с параметром ![]() . Параметры состояний
равны:
. Параметры состояний
равны: ![]() ,
, ![]() ,
, ![]() .
.
2. Решение: Состояния автомашин:
![]() –
машина исправна;
–
машина исправна;
![]() –
машина ожидает ремонта;
–
машина ожидает ремонта;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.