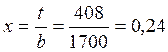Задача расчета потребной складской площади методами теории массового обслуживания. Задача выбора технических решений в условиях неопределённости и риска, страница 3

.

  II.  Вероятность безотказной работы для закона Вейбулла определяется по формуле:

;

.

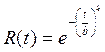  III.  Средняя наработка до отказа определяется как:

;

.

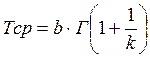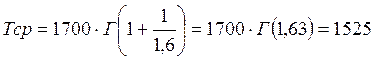  IV.  Интенсивность отказов определяется по следующей формуле:

;

.

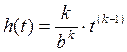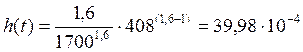  V.  Плотность вероятности отказов определяется как:

;

.

Произведённые расчёты по всем вариантам  t  приведены в таблице 5.1.

			*10
408	0,24	0,903	39,98	36,1
816	0,48	0,733	60,5	44,35
1224	0,72	0,552	77,29	42,66
1632	0,96	0,390	91,85	35,82
2040	1,2	0,261	105	27,41
2448	1,44	0,165	117,14	19,33
2856	1,68	0,099	128,49	12,72
3264	1,92	0,058	139,21	8,07
3672	2,16	0,032	149,41	4,78
4080	2,4	0,017	159,16	2,71

Графические зависимости характеристик надёжности от наработки представлены на рисунках 5.1 – 5.3.

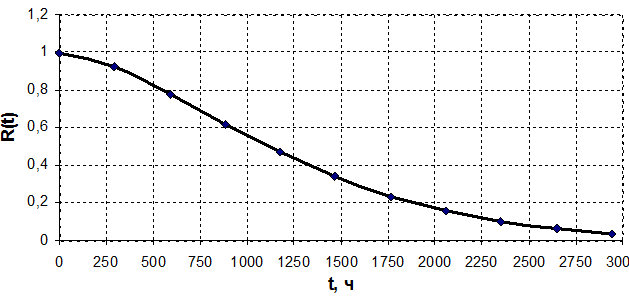
Рисунок 5.1 – Зависимость вероятности безотказной работы по закону Вейбулла от времени

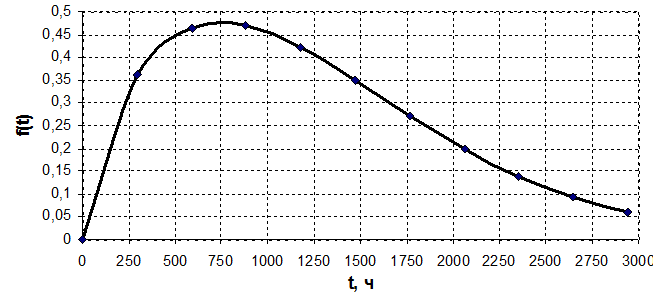
Рисунок 5.2 – Зависимость плотности вероятности отказа от времени

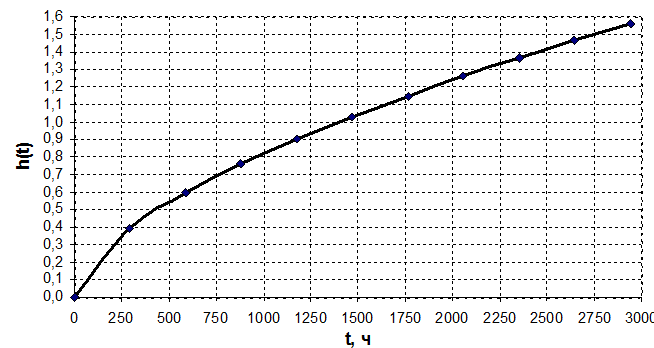
Рисунок 5.3 – Зависимость интенсивности отказов от времени

Задача №6

Задача определения готовности отправления поездов по графику

1.  Постановка задачи: Определить готовности отправления поездов по графику и надёжность графика отправления поездов, если на надёжность отправления влияют семь компонентов.

2.  Решение:

  I.  Коэффициент готовности отправления поезда по графику определяется по формуле:

.

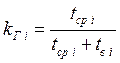Следовательно:

1	0,9723
2	0,98
3	0,9819
4	0,9695
5	0,9838
6	0,9819
7	0,9876

  II.  Коэффициент надёжности выполнения графика поездов определяется по данной формуле:

;

.

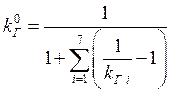  III.  Надёжность выполнения графика движения поездов по направлению определяется как:

.

Надёжность выполнения графика не высока из-за неудовлетворительной величины коэффициента готовности по комплексам.

3.  Вывод: предположив, что за сутки проходит 100 поездов, то получим число сорванных с графика поездов равно 13.

Задача №7

Задача выбора технических решений в условиях неопределённости и риска