Задача расчета потребной складской площади методами теории массового обслуживания. Задача выбора технических решений в условиях неопределённости и риска, страница 2

 – машина находится в ремонте.

Граф состояний машины имеет вид:

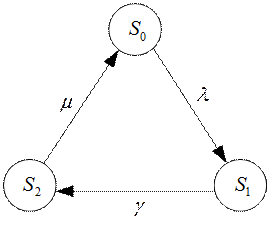
Для вероятностей  составим систему дифференциальных уравнений с переменными коэффициентами (уравнения Колмогорова).

  I.  Уравнения Колмогорова составляются по следующему мнемоническому правилу: производная вероятности любого состояния равна сумме потоков вероятностей, переводящих систему в это состояние и минус сумма всех потоков вероятности, выводящих из этого состояния.

В соответствии с графом и мнемоническим правилом система будет иметь следующий вид:

Систему ДУ решают при начальных условиях, задающих вероятности состояний в начальный момент времени при :

.

Причём для любого момента времени  выполняется нормировочное условие:

,    .

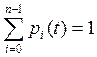  II.  Вместо первого дифференциального уравнения используем нормировочное условие:

.

В данном примере начальные условия примем равными:

;          .

  III.  Решим данную задачу методом Рунге-Кутта.

Решение задачи методом Рунге-Кутта приведено в приложении А.

Вывод: вероятность исправности автомашины составляет 0,328, вероятность ожидания ремонта – 0,179, вероятность нахождения в ремонте – 0,493.

Задача №4

Задача оценки надёжности не восстанавливаемых изделий по статическим данным

1.  Постановка задачи: На испытание поставлено 860 образцов невосстанавливаемого изделия . Число отказов () регистрировали через каждые 135 часов (). Требуется вычислить количественные показатели надежности изделия и построить их зависимость от времени.

2.  Решение:

  I.  Вероятность безотказной работы определяется по следующей формуле:

;

.

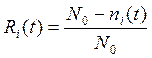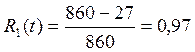  II.  Частота отказов в интервале времени определяется как:

;

.

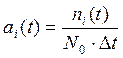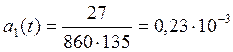  III.  Среднее число, исправно работающих изделий в интервале времени определяется по данной формуле:

;

.

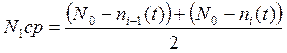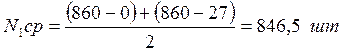  IV.  Интенсивность отказа в интервале времени находится как:

;

.

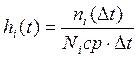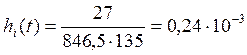Произведённые расчёты приведены в таблице 2.

Таблица 4.1 – Расчёт количественных показателей надёжности изделия

t	ni(^t)	ni(t)	Ri(t)	ai(t)	Ncp	hi(H)
0	0	0	1	0	0	0
135	27	27	0,969	0,00023	846,5	0,00024
270	38	65	0,924	0,00033	814	0,00035
405	10	75	0,913	0,00009	790	0,00009
540	49	124	0,856	0,00042	760,5	0,00048
675	42	166	0,807	0,00036	715	0,00044

Зависимости количественных показателей от времени приведены на рисунках 4.1 и 4.2.

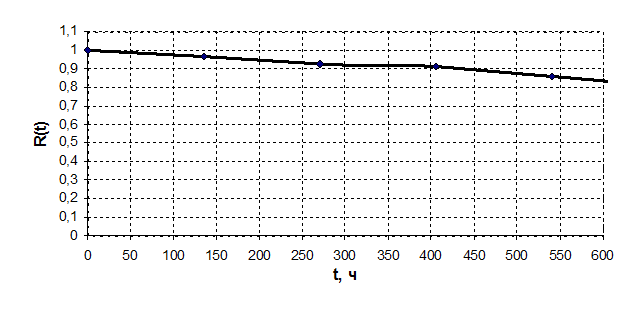
Рисунок 4.1 – Зависимость вероятности безотказной работы от времени

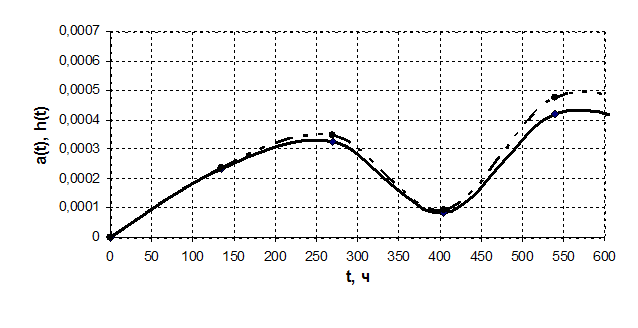
Рисунок 4.2 – Зависимости частоты и интенсивности отказа работы от времени

Задача №5

Задача прогнозирования надёжности невосстанавливаемого изделия

1.  Постановка задачи: Зависимость наработки устройства до отказа от времени его эксплуатации подчиняется закону Вейбулла с параметрами , . Требуется вычислить количественные характеристики надёжности устройства в интервале времени его работы от 0 до 4080 ч с дискретностью  и определить результаты в виде графических зависимостей характеристик надёжности от наработки.

2.  Решение:

  I.  Одна из характеристик определяется как: