Моделирование станционных технологий с помощью сетевого планирования

Задача №1 (вариант 4)

Задача моделирование станционных технологий с помощью сетевого планирования.

Рассматривается технологическая линия переработки транзитных вагонов на сортировочной станции. Для заданного сетевого графика комплекса работ по переработке вагонов на станции определить:

1)  плановое время начала работы

2)  Критический путь и его длину

3)  Полные и свободные резервы времени выполнения работ

 

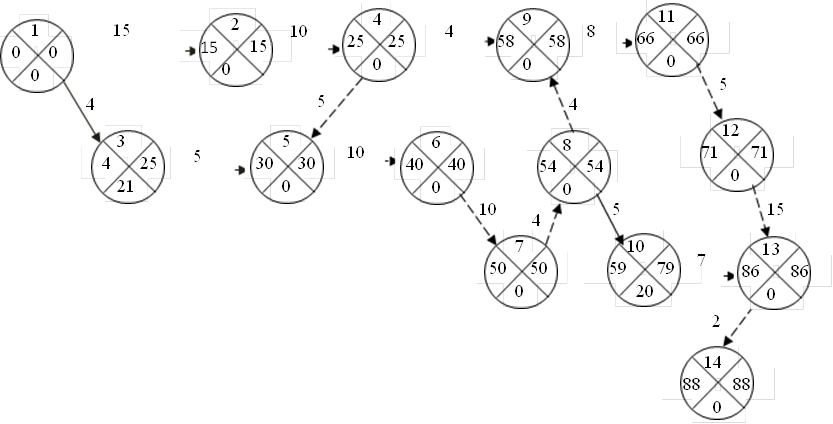
Рисунок 1.1 – сетевой график

Вычислим ранние сроки совершения всех событий.

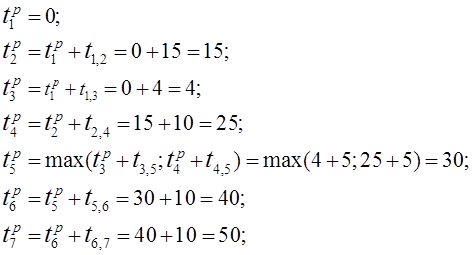
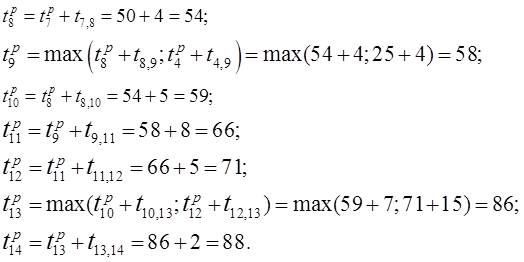
Вычислим поздние сроки совершения всех событий.

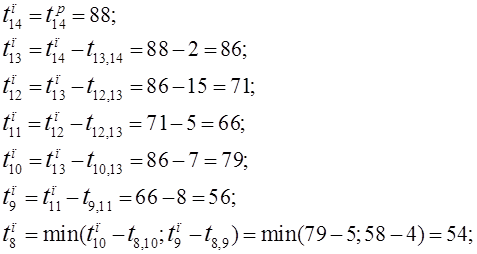
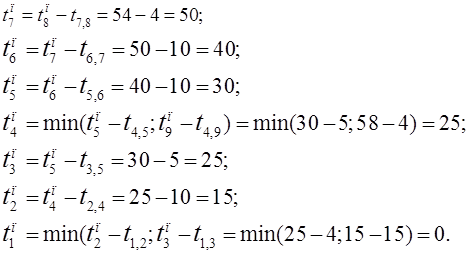
Проложим критические пути:

1-2-4-9-11-12-13-14;

1-2-4-5-6-7-8-9-11-12-13-14

Их продолжительности равны:

единиц времени

единиц времени

Для работ, не лежащих на критическом пути, вычислим полные и свободные резервы времени выполнения работ.

      

Работы (i;j)
(1;3)	25-0-4=21	4-0-4=0
(3;5)	30-25-5=0	30-4-5=21
(8;10)	79-54-5=20	59-54-5=0
(10;13)	86-79-7=0	86-59-7=20

Вывод: произведен расчет параметров сетевого графика. Критические пути пролегают через события 1,2,4,9,11,12,13,14 и 1,2,4,5,6,7,8,9,11,12,13,14 их длина составляет 59 и 88 единиц времени. Работы не лежащие на критическом пути имеют резервы времени, следовательно, необходимые ресурсы для их выполнения могут быть использованы на других участках работ.

Задача №2 (вариант 4)

Задача моделирование станционных технологий с помощью сетевого планирования.

Рассматривается технологическая линия переработки транзитных вагонов на сортировочной станции. Для заданного сетевого графика комплекса работ по переработке вагонов на станции определить:

1.Плановое время начала работы

2.Критический путь и его длину

3.Определение резерв времени некритических работ

Исходные данные.

 

Рисунок 2.1 – сетевой график

1.  Построим линейный график выполнения комплекса работ по известным продолжительностям выполнения каждой работы.

Рисунок 2.2 – линейный график выполнения комплекса работ

2.  По линейному графику находим критический срок выполнения работ.

Работа (13;14), будучи завершающей работой комплекса, является критической. Непосредственно ей предшествует работа (12;13), (11;12), (9;11), (8;9), (7;8), (6;7), (5;6), (4;5), (2;4), (1;2). Следовательно, работы (12;13), (11;12), (9;11), (8;9), (7;8), (6;7), (5;6), (4;5), (2;4), (1;2) являются критическими, а остальные – некритическими.

Путь 1-2-4-5-6-7-8-9-11-12-13-14- критический.

3.Определим резервы времени некритических работ. 

Не критические работы:

9-11,8-10,4-9,3-5,1-3.

Вывод: все подготовительные работы, связанные с переводом производства на более интенсивную технологию, займут 88 единиц времени. Работы имеют резервы времени, следовательно, необходимые ресурсы на их выполнение можно использовать для других задач станционной технологии.

Задача №3 (вариант 4)

Задача минимизации издержек производства с применением графического способа и метода множителей Лагранжа.

Постановка задачи

По плану производства продукции предприятию необходимо изготовить 130 изделий. Эти изделия могут быть изготовлены двумя технологическими способами. При производстве  изделий первым способом затраты равны  (ден.ед.), при изготовлении  изделий вторым способом затраты равны   (ден.ед.). Определить сколько изделий каждым из способов следует изготовить так, чтобы общие затраты на производство продукции были минимальными.

Требуется:

1)  Составить математическую модель

2)  Решить задачу графическим способом

3)  Решить задачу методом множителей Лагранжа

4)  Сделать вывод

1.  Составим математическую модель

     

2.  Решим задачу графическим способом

Находи решение задачи используя графическую интерпретацию.

 

Функция  достигает своего минимума при тех же значениях  и  , что и функция     

Областью допустимых решений является отрезок АВ, а линиями уровня являются окружности с центром в точке Е(-1:-1/2).

                   

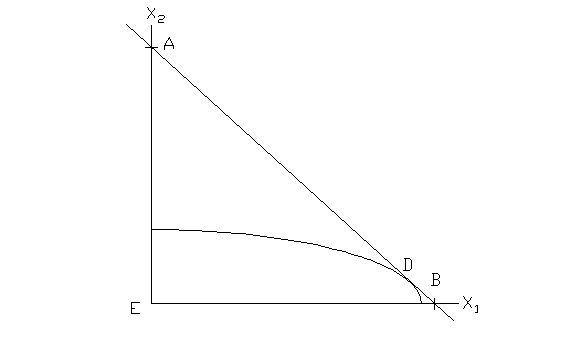
Из рисунка видно, что минимальное значение функции достигается в точке Д. 

Чтобы найти координаты этой точки, воспользуемся тем, что угловой коэффициент касательной к окружности  совпадает с угловым коэффициентом прямой.

Рассматривая  как неявную функцию от  дифференцируем уравнение окружности.

      

 

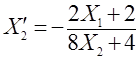
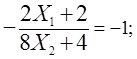
3.  Метод неопределённых множителей Лагранжа.

Вычислим частные производные  функции по ,  и . Приравняем их к нулю и решим полученную систему уравнений.

      

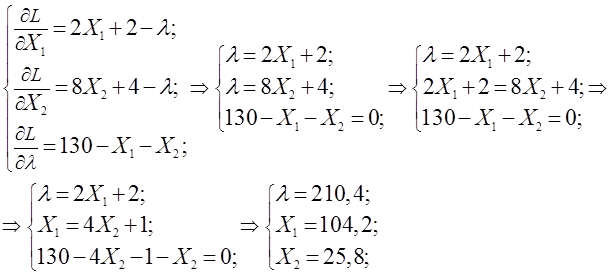
Определим минимальные затраты:

Вывод: если предприятие изготовит 104 изделия первым технологическим способом и 26 изделий вторым способом, то общие затраты будут минимальными и составят 13832 ден.ед.

Задача №4 (вариант 4)

Задача минимизации издержек производства градиентным методом.

Постановка задачи

Предприятие выпускает два вида продукции в объемах Х₁ и Х₂. Функция определяет себестоимость производства продукции. Требуется улучшить начальный план 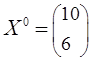, (где Х₁=10, Х₂=6) производства продукции с целью минимизации издержек производства; решить задачу методом наискорейшего спуска, выполнив две итерации вычислительного процесса.

1 итерация

1). Проверим условие оптимальности для точки Х⁰. Вычислим градиент в точке .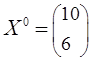

   

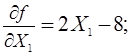
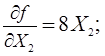
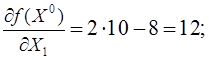
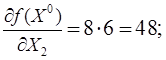
Градиент не равен нулю, следовательно текущее приближение не является точкой минимума.

2). Вычислим шаг  из следующего соотношения для обводимой функции .

  

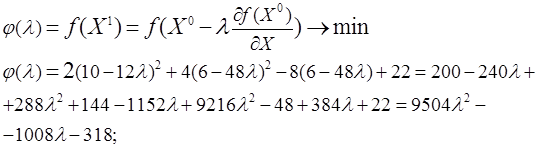
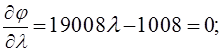
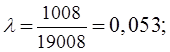
3). Переходим к точке Х¹(;).

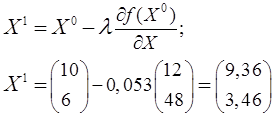
Проверим условие оптимальности для Х¹.

 

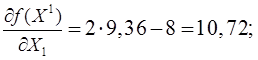
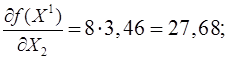
Градиент не равен нулю, следовательно текущее приближение не является точкой минимума.

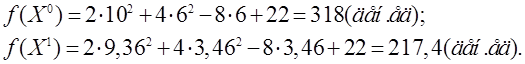
Определив значение целевой функции в точках Х⁰ и Х¹ увидим, что

, следовательно выполняем вторую итерацию и переходим к точке Х², повторяя шаги предыдущей итерации.

2 итерация

 

  

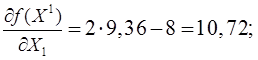
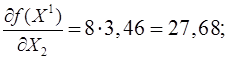
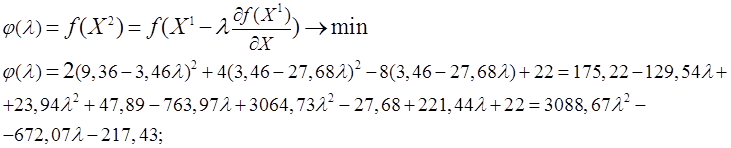
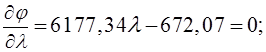
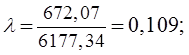
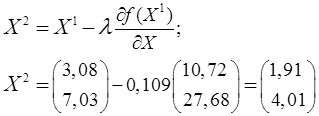
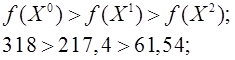
Вывод: в результате выполнения двух итераций вычислительного процесса определили, что улучшенный план производства с целью минимизации издержек производства будет следующий: предприятие должно выпускать два вида продукции в объемах Х₁=1,91 ед. и Х₂=4,01 ед.