Задача на Марковские системы обслуживания

Задача №2

Задача на Марковские системы обслуживания

Дано: В вокзальном помещении находится 3 билетные кассы. В среднем за час в них обращается 40 человек, а каждый из кассиров обслуживает одного пассажира в среднем 3 мин. Поступающий в кассу поток пассажиров предполагается простейшим, а время обслуживания распределенным экспоненциально. Считается, что образованная пассажирами очередь будет общей для всех касс. Найти вероятность того, что длина общей очереди к кассам не превысит 5 человек. Процесс обслуживания считать стационарным.

Решение: Билетная касса является марковской системой: М/М/3.

Интенсивность входящего потока   чел/ч, а интенсивность обслуживания    чел/ч (при работе одной кассы).

Коэффициент загрузки системы:

.

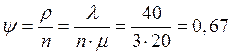Найтем вероятность того, что длина общей очереди к кассам не превысит 5 человек (n=8):

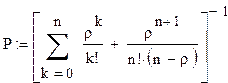
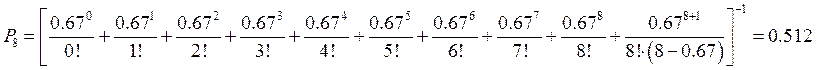 Вероятность того, что длина общей очереди к кассам не превысит 5 человек 0,512.