Использование алгоритма решения задач нелинейного программирования

Вариант №8

Задание №3

Использование алгоритма решения задач нелинейного программирования.

Цель задания минимизация издержек производства с применением графического способа и метода множителей Ла-Гранжа

Требуется:

1. Записать постановку задачи.

2. Записать математическую модель.

3. Решить задачу графическим способом.

4. Решить задачу методом множителей Ла-Гранжа

5. Проанализировать решение, сделать вывод.

Выполнение задания:

1. По технологическому графику работы сортировочной горки необходимо распустить 180 составов. Составы могут быть распущены двумя способами. При роспуске  составов с осаживанием вагонов ЗСГ затраты времени составят  мин, а при роспуске  составов со снятием вагонов ЗСГ затраты времени составят мин.

Определить сколько составов необходимо распустить каждым способом, чтобы общие затраты времени были минимальными.

2. Запишем математическую модель задачи.

;

;

;

.

Решим задачу графическим способом.

Преобразуем целевую функцию:

;

;

.

Таким образом, получили уравнение окружности с центром в точке с (-2;-2).

Графически условие задачи будет выглядеть следующим способом:

Предположим, что зависит от . Возьмем производную по :

;

Из полученного уравнения выразим :

;

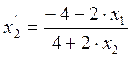Т.к. , то получим:

;

;

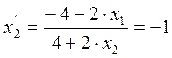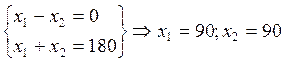составов.

4. Решим задачу методом множителей Ла-Гранжа.

Предположим, что условие неотрицательности на и не налогается. Тогда:

;

Определим производные по , ,и приравняем их к нулю:

;

;

;

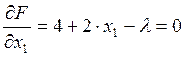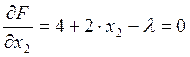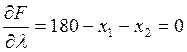Так как правые части первых двух производных равны, то можем приравнять левые части:

;

Учитывая последнюю производную, получим систему уравнений:

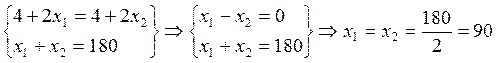составов.

Отметим, что полученное решение удовлетворяет условию неотрицательности и ограничениям задачи.

5. Решив данную задачу определили, что при работе сортировочной горки необходимо распустить 90 составов с осаживанием вагонов ЗСГ и 90 составов со снятием вагонов ЗСГ, тогда общие затраты времени на роспуск всех составов будут минимальны.

Таким образом длина  критического пути 1-2-6-8-9-10 составляет 35 вр.е.

Определим резервы  времени работ.

Для работы (1-4):

Полный резерв времени:

Ri,j= Tl,j-( Te,i+ ti,j)

Ri,j= 11-(0+ 4)=7

Свободный резерв времени:

Ri,jс= Tе,j-( Te,i+ ti,j)

Ri,jс= 10-( 0+ 4)=6

Независимый резерв времени:

Ri,jн= Tе,j-( Tl,i+ ti,j)

Ri,jн= 10-( 0+ 4)=6

Остальные расчеты приведены в таблице 1.

Таблица 1 – Резервы времени работ

№	Полный резерв времени (Ri,j)	Свободный резерв времени (Ri,jс)	Независимый резерв времени (Ri,jн)
(1-4)	7	6	6
(1-3)	4	0	0
(2-4)	1	0	0
(3-5)	4	3	-1
(4-5)	1	0	-1
(4-7)	14	13	12
(5-7)	1	0	-1
(6-7)	9	8	8
(6-9)	13	13	13
(7-10)	1	1	0
(5-10)	13	13	12

Составим линейную диаграмму для определения максимального количества бригад.

С целью уменьшения количества бригад можно внести следующие предложения по календарному плану:

1. Работу (6-9) начать не в 12 вр.е., а в 15 вр. е. Этим мы сможем на интервале от 12 до 14 вр.е. уменьшить количество бригад с 5 до 4-х. На интервале с 15 до 17 вр.е. количество бригад увеличится с 3-х до 4-х.

2. Работу (5-10) начать не в 18 вр.е. а  в 30 вр.е. Это позволит на участке от 18 до 22 вр.е. снизить количество бригад с 3-х до 2-х. На интервале с 30 до 34-х вр.е. количество бригад увеличится с 2-х до 3-х.

3. Работу (6-7) начать не в 12 вр.е. а  в 18 вр.е. Это позволит на участке от 12 до 17 вр.е. снизить количество бригад с 4-х до 3-х. На интервале с 18 до 23-х вр.е. количество бригад увеличится с 2-х до 3-х.

4. Работу (4-7) начать не в 10 вр.е. а  в 23 вр.е. Это позволит на участке от 10 до 12 вр.е. снизить количество бригад с 4-х до 3-х. На интервале с 23-х до 25 вр.е. количество бригад увеличится с 2-х до 3-х.

Предложенные варианты выполнения работ позволят снизить количество одновременно работающих бригад с 5-ти до 3-х.

Определим наиболее экономичный маршрут:

Наиболее экономичный маршрут 1-4-7-10 составляет 15 вр.е.