Задача № 5
ПРОГНОЗИРОВАНИЕ НЕВОССТАНАВЛИВАЕМЫХ ИЗДЕЛИЙ
1 Постановка задачи. Зависимость наработки устройства
до отказа от времени его эксплуатации подчиняется двухпараметрическому закону
Вейбула с параметрами k = 1.6 иb = 1700 часов.
Требуется вычислить количественные характеристики надежности устройства в
интервале времени его работы ![]() ч с дискретностью
ч с дискретностью ![]() ч и представить результаты в виде
графических зависимостей характеристик надежности от наработки.
ч и представить результаты в виде
графических зависимостей характеристик надежности от наработки.
2 Решение. При выполнении задания будем использовать известные из курса математической статистики формулы для расчета показателей надежности, так как распределение наработки изделия до отказа подчиняется закону Вейбула. Вычисления будем выполнять в табличной форме.
Рассмотрим порядок вычисления показателей надежности для наработки t = 408 ч. Вычислим характеристику x = t/b:
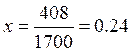 .
.
Вероятность безотказной работы P(t) для закона Вейбула определяется по формуле:
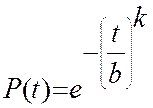
Подставив численные значения t/b и k получим P(t) = e- 0.24^1.6. Находим P(408)=0.903.
Интенсивность отказов для заданного закона определяется по формуле:
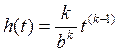 ,
,
откуда получаем h(408) = 1.6/17001.6 · 4081.6-1 = 0.0003998 ч.
Плотность вероятности отказов для закона Вейбула находим по формуле:
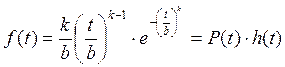 .
.
Подставив численные значения параметров, f(408) = 0.903 · 0.0003998 = 3.61 · 10-4. Расчет для других наработок сведем в таблицу.
Таблица – Вероятностная оценка количественных показателей надежности устройств при распределении наработки по закону Вейбула
|
t,ч |
t/b |
P(t) |
h(t)*10^ -4,ч^ -1 |
f(t)*10^ -4 |
|
408 |
0,24 |
0,903 |
3,998 |
3,61 |
|
816 |
0,48 |
0,734 |
6,059 |
4,45 |
|
1224 |
0,72 |
0,554 |
7,728 |
4,28 |
|
1632 |
0,96 |
0,392 |
9,184 |
3,60 |
|
2040 |
1,2 |
0,262 |
10,5 |
2,75 |
|
2448 |
1,44 |
0,167 |
11,71 |
1,96 |
|
2856 |
1,68 |
0,101 |
12,85 |
1,30 |
|
3264 |
1,92 |
0,058 |
13,92 |
0,81 |
|
3672 |
2,16 |
0,032 |
14,94 |
0,48 |
|
4080 |
2,4 |
0,017 |
15,92 |
0,27 |
Средняя наработка изделия на отказ вычисляется по формуле:
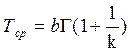 ,
,
где Г – гамма – функция.
В нашем случае
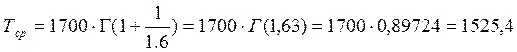 ч.
ч.
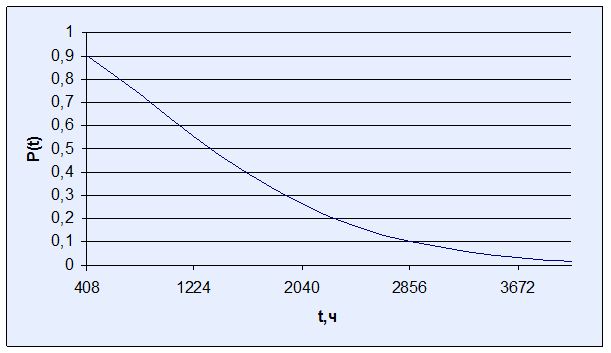
Зависимость вероятности безотказной работы изделия от наработки
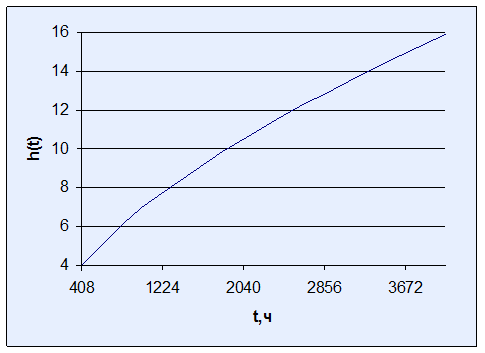
Зависимость интенсивности отказов работы изделия от наработки
Зависимость частоты отказов изделия от наработки
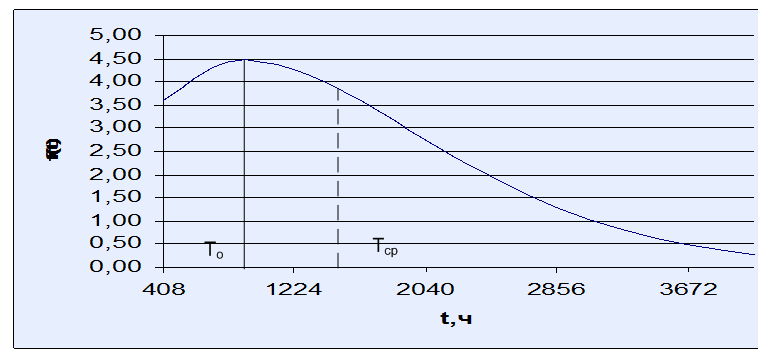
3 На рисунках изображены графики функций P(t), h(t) и f(t). Как видно из рисунков, функция P(t) является убывающей, а h(t) – возрастающей. Функция плотности распределения f(t) наработки до отказа имеет, как правило, куполообразный вид, и ее максимуму соответствует мода наработки устройства до отказа То ≈ 920 ч.
Другим характерным параметром функции f(t) является средняя наработка до отказа Тср≈1525,4 ч: прямая t = Тср = const делит площадь, заключенную между кривой f(t) и осью (0;t), на две равные части.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.