Минимизация
издержек производства с помощью градиентного метода
Предприятие
выпускает два вида продукции, в объёмах и . Функция (д.е.)
определяет себестоимость производства продукции. Требуется улучшить начальный
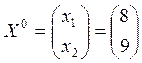план производства, с целью минимизации издержек
производства. Решим задачу используя градиентный метод и выполним две итерации
вычислительного процесса.
Решение:
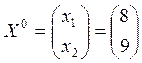
1) Вычислим градиент функции f в
точке .
; ; ; .
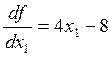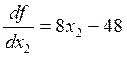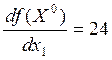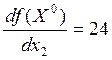Так как
градиент не равен нулю, то точка приближения не является точкой минимума.
2) Вычислим
шаг исходя из следующего соотношения для
вводной функции.
;
;
;
;
;
.
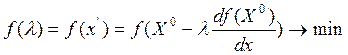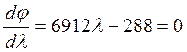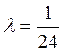3) Переходим
к точке .
;
;
.
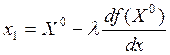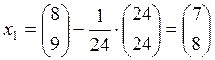4)
Проверим
условие относительности.
; .
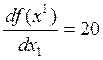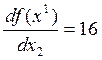Так как
градиент не равен нулю, то точка не является точкой min.
5) Переходим
к точке .
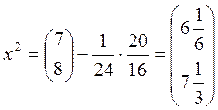
6) Определив
значение целевой функции в точках видим, что
и 
. Функция 
(д.е.)
определяет себестоимость производства продукции. Требуется улучшить начальный
план 
производства, с целью минимизации издержек
производства. Решим задачу используя градиентный метод и выполним две итерации
вычислительного процесса.
.
; 
; 
; 
.
исходя из следующего соотношения для
вводной функции. 
;
;
;
;
;
.
.
;
;
.
; 
.
.
видим, что 
