Задача№1
Задание: Решить задачу построения наиболее экономного маршрута перевозки грузов по сети.
Требуется:
1. Записать постановку задачи.
2. Разбить пункты сети на группы.
3. Методом динамического программирования найти наиболее экономичный маршрут доставки груза.
4. Проанализировать решение, сделать вывод.
1. На данной сети дорог (рис. 1) указаны стоимости доставки единицы груза из пункта в пункт. Найти наиболее экономный маршрут перевозки груза из первого пункта в двенадцатый.
Рисунок 1.1 – Сеть дорог доставки груза.
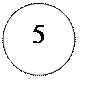
 2
2
![]()


![]()
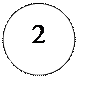 4
4
![]()

 4
4

 2
2
2
2
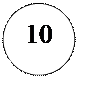



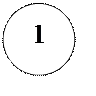

 8
8
3
 7
7
![]() 3
3
![]() 1 5
1 5


 6
6
5 3
![]() 9
9

3 7
 8
8
1
![]()
2. Разбиваем пункты сети на группы.
|
I |
II |
III |
IV |
V |
|
1 |
2 |
5 |
9 |
12 |
|
3 |
6 |
10 |
||
|
4 |
7 |
11 |
||
|
8 |
Состояние ![]() - факт нахождения груза в пункте.
- факт нахождения груза в пункте.
Управление –
выбор направления движения ![]() .
.
Физическая система S – сеть дорого и транспорт с грузом.
Целевая
функция ![]() - минимальные затраты.
- минимальные затраты.
![]() - результирующее значение целевой функции
с учетом выбора управления на данном шаге и выбор управления на последующем
шаге.
- результирующее значение целевой функции
с учетом выбора управления на данном шаге и выбор управления на последующем
шаге.
3. Находим наиболее экономичный маршрут доставки груза.
I. Этап условной оптимизации
i=4
|
|
|
|
|
|
|
(9-12) |
|
2 |
|
|
(10;12) |
3 |
|
|
|
(11;12) |
7 |
i=3
|
|
|
|
|
|
|
|
|
(5-9) (5-10) |
|
2 8 |
2 3 |
4 11 |
|
|
(6-9) |
|
4 |
2 |
6 |
|
|
(7-10) (7-11) |
|
6 3 |
3 7 |
9 10 |
|
|
(8-11) |
|
1 |
7 |
8 |
|
|
|
|
|
|
|
|
|
(1-2) (1-3) (1-4) |
|
3 1 5 |
8 6 11 |
11 7 16 |
i=2
|
|
|
|
|
|
|
|
|
(2-5) (2-7) |
|
4 7 |
4 9 |
8 16 |
|
|
(3-5) (3-8) |
|
2 9 |
4 8 |
6 17 |
|
|
(4-6) (4-7) (4-8) |
|
5 9 8 |
6 9 8 |
11 18 16 |
i=1
II. Этап безусловной оптимизации.
1-3-5-9-12
Подсчитаем минимальные затраты на перевозку груза по данному маршруту:
![]() 1+2+2+2=7 д.е.
1+2+2+2=7 д.е.
4. Вывод: С помощью метода динамического программирования определили маршрут доставки груза из пункта 1 в пункт 12, при этом минимальные затраты составят 7 д.е.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.