Нахождение наивыгоднейшего режима ведения поезда по участкам

Задача№2.вар10.

Нахождение наивыгоднейшего режима ведения поезда по участкам.

Постановка задачи:

Необходимо определить такой режим следования поезда на отрезках пути, который обеспечил бы минимальные приведенные расходы на  передвижение по участка в целом.

Решение:

Приведенные расходы зависят от скорости поезда и от сопротивления его движению, которое в свою очередь зависит от профиля пути. Поэтому, в качестве вычислительного этапа можно рассматривать элемент профиля пути с одинаковым уклоном. На рис.1 изображен график нахождения наивыгоднейшего режима, на котором базируется наше решение.

Начинаем решать задачу с конца  поэтапно. На последний элемент поезд может вступить с тремя значениями скорости. Каждому из которых однозначно соответствуют приведенные расходы на передвижение поезда по этому участку до остановки. Выделяем три условно оптимальных стратегии:

=50; =55; =70 на предпоследний элемент (вертикаль №6) поезд может вступить также с тремя значениями скорости, но и двигаться он может в одну из трех точек на вертикали №7 по трем режимам. Находим условно оптимальные стратегии на этом элементе: .

;

;

Аналогично находим условно оптимальные стратегии.

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

Поскольку на последнем этапе расчетов состояние системы задано однозначно, определим лишь одно значение:

;.

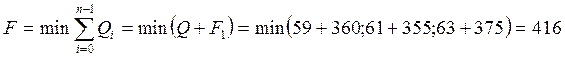Теперь начиная с первой точки и проходя последовательно по непрерывной ломаной жирной линии. Определим оптимальную стратегию в целом для всего процесса и на каждом элементе:

;

45+70+35+26+50=392

Вывод: при данном режиме движения поезда будут минимальные приведенные расходы на передвижение по участку в целом.