Планирование перевозки грунта потребителям так, чтобы суммарные затраты на разработку и перемещение грунта были минимальны

ТРАНСПОРТНАЯ ЗАДАЧА В МАТРИЧНОЙ ФОРМЕ

Задание. Решить транспортную задачу в матричной форме:

1. Записать постановку задачи.

2. Установить тип модели транспортной задачи.

3. Записать математическую модель.

4. Построить начальный план перевозок известным Вам методом, проверить, является ли он базисным. Определить его общую стоимость.

5. Методом потенциалов найти оптимальный план и определить его общую стоимость.

6. Сделать вывод.

Краткие теоретические сведения

Рассмотрим некоторые практические задачи.

З1. На m станциях отделения железной дороги имеется избыток порожних вагонов одного вида, запасы которых составляют соответственно А₁, А₂, … А_m ед., а на n станциях их не хватает. Требуется так распределить порожние вагоны на станции недостатка, спрос которых равен соответственно В₁, В₂, … В_n, чтобы пробеги порожних вагонов были минимальны. Расстояния от станций избытка до станций недостатка известны.

З2. Запасы поставщиков земляного грунта составляют соответственно А₁, А₂, … А_m ед. Требуется так спланировать перевозки грунта потребителям, спрос которых равен соответственно В₁, В₂, … В_n так, чтобы суммарные затраты на разработку и перемещение грунта были минимальны. Стоимости разработки и перемещения единицы грунта c_ij (i=1…m, j=1…n) от i - го поставщика к j - му потребителю с учётом различных способов производства земляных работ и дальности перемещения грунта известны.

1. В общем виде ТЗ формулируется следующим образом:

Пусть имеется m  поставщиков, располагающих некоторым однородным продуктом в объемах по А_i единиц (i=1…m), и n получателей с объемами потребления по В_j единиц ( j=1…n). Задана матрица C=||c_ij||, где c_ij - стоимость перевозки единицы продукции от i -го поставщика j-му потребителю. Возникает задача нахождения плана перевозок Х=||х_ij||, где х_ij - количество единиц продукции, поставляемой по коммуникации ij. Целевой функцией можно считать суммарную стоимоcть всех перевозок. Условия задачи принято записывать в таблице следующего вида:

Таблица __.1. Матрица затрат на перевозку единицы продукции

Замечание 1. Величины c_ij  задаются в зависимости от того, какую именно функцию необходимо минимизировать. Это может быть расстояние, время доставки груза, заработная плата, расход электроэнергии и т.п. 

Замечание 2. Задача является задачей закрытого типа, если суммарный объем избытков у поставщиков равен суммарному спросу потребителей. В противном случае говорят о задаче открытого типа.

Транспортная задача - это частный случай ОЗЛП. Поэтому для ее решения пригоден любой метод решения задачи линейного программирования и, в частности, универсальный метод - симплексный.

Однако, его применение в данном случае не оправдано, так как значительно усложняет процесс решения. Транспортные задачи решают специальными методами. Методы решения ТЗ можно разбить на две группы: 1) последовательного улучшения начального базисного плана; 2) последовательного сокращения невязок. К первой группе относятся распределительный метод, метод потенциалов и его модификации. Их сущность состоит в том, что сначала определяется некоторый начальный базисный план и затем от итерации к итерации он улучшается, пока через конечное число итераций не будет получен оптимальный план. Ко второй группе причисляют методы дифференциальных рент, разрешающих слагаемых, венгерский метод и др. Здесь вначале устанавливается наилучший (в смысле затрат) план, но не допустимый (так называемый условно-оптимальный). Затем от итерации к итерации из условно-оптимального он переводится в оптимальный..

Подробно рассмотрим наиболее эффективный метод первой группы - метод потенциалов, предложенный советским математиком Л.В.Канторовичем.

2. Метод потенциалов предполагает, что ТЗ является задачей закрытого типа, т.е. выполняется условие общего баланса

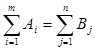                                                (__.1)

В случае, если суммарные запасы поставщиков больше потребностей получателей, вводят (n +1)-го фиктивного потребителя, потребности которого равны излишку запаса, т.е.

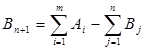                                          (__.2)

Стоимости перевозки единицы продукции от i -го поставщика