Оценка показателей надежности изделия невосстанавливаемого элемента и построение графиков их зависимости от времени. Определение общего коэффициента готовности отправления поездов по графику

Задача №1

На испытание поставлено n₀ образцов невосстанавливаемого изделия. Число отказов N₀∆t регистрировали через каждые ∆t часов испытаний. Требуется оценить показатели надежности изделия невосстанавливаемого элемента и построить графики их зависимости от времени.

N0	∆t	n1(∆t)	n2(∆t)	n3(∆t)	n4(∆t)	n5(∆t)
1250	145	68	31	19	50	74

Найдем число изделий, вышедших из строя к моменту накопления:

Число изделий, вышедших из строя к моменту накопления

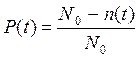
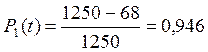
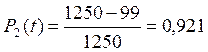
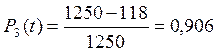
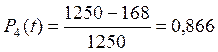
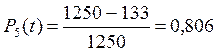
Оценим показатели надежности изделия:

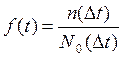
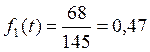
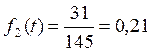
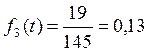
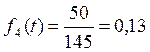
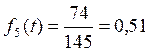
Среднее число изделий:

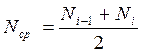
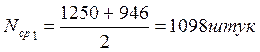
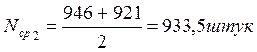
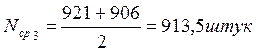
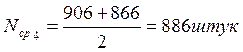
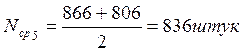
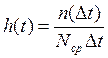
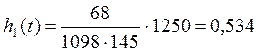
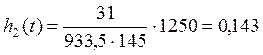
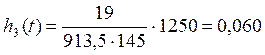
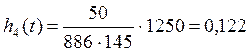
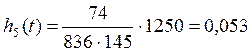
t, ч	n(∆t), штук	n(t)	P(t)	f(t), 10-3час-1	Nср, штук	h(t)
145	68	68	0,946	0,38	1098	0,534
290	31	99	0,921	0,17	933.5	0,143
435	19	118	0,906	0,10	913.5	0,060
580	50	168	0,866	0,28	886	0,122
725	74	242	0,806	0,41	836	0,153

Графики f(t), 10^-3час^-1 . P(t), h(t)

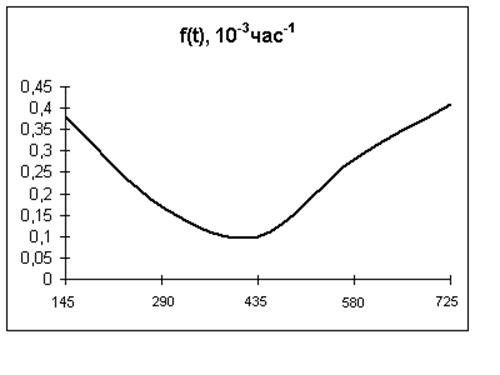
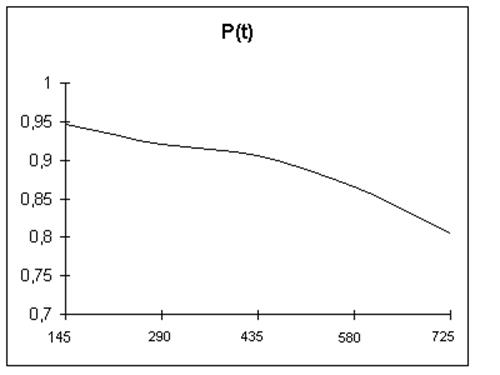
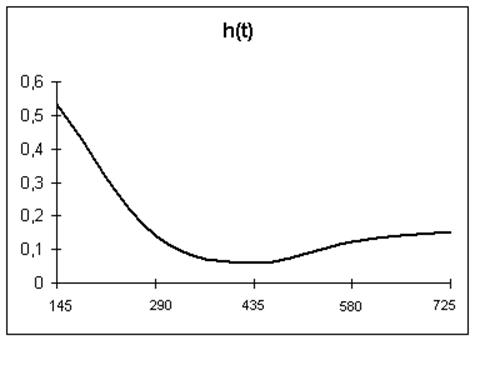
Задача№2

Зависимость наработки изделия на отказ от времени его эксплуатации описывается двухпараметрическим законом Вейбулла. Требуется вычислить показатели надежности работы изделия на промежутке [0,t_max] с дискретностью 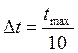. Результаты представить в табличном виде и графически.

tmax, ч	b, ч	k
4200	2000	1,8

Найдем интенсивность отказов по формуле:

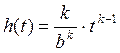
Представляем в табличном виде:

t, ч	P(t)=1-F(t)	h(t), 10-4час-1	f(t), 10-4час
0	1	0	0
420	0,941	2,6	2,44
840	0,811	4,5	3,65
1260	0,647	6,2	4,01
1680	0,481	7,8	3,75
2100	0,335	9,4	3,14
2520	0,219	10,8	2,36
2940	0,135	12,2	1,64
3360	0,078	13,6	1,06
3780	0,043	15,0	0,64
4200	0,022	16,3	0,35

Дискретность промежутка времени:

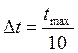
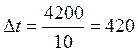
Найдем интенсивность отказов:

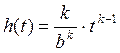
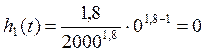 ∙ 10^-4час^-1

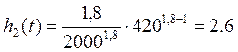 ∙ 10^-4час^-1

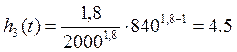 ∙ 10^-4час^-1

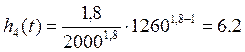 ∙ 10^-4час^-1

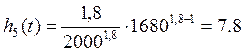 ∙ 10^-4час^-1

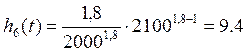 ∙ 10^-4час^-1

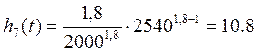 ∙ 10^-4час^-1

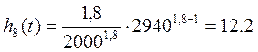 ∙ 10^-4час^-1

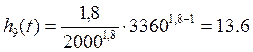 ∙ 10^-4час^-1

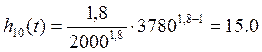 ∙ 10^-4час^-1

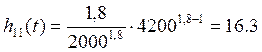 ∙ 10^-4час^-1

Частота отказов:

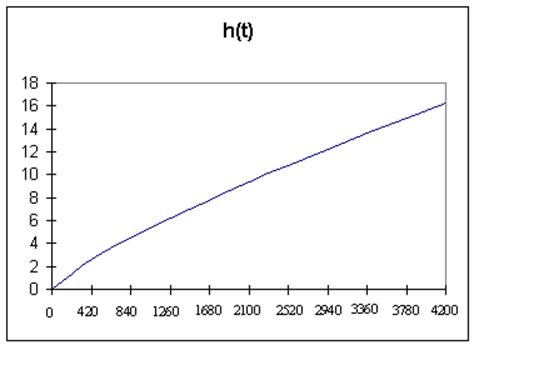
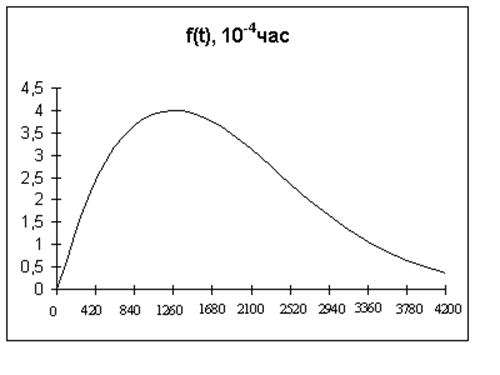
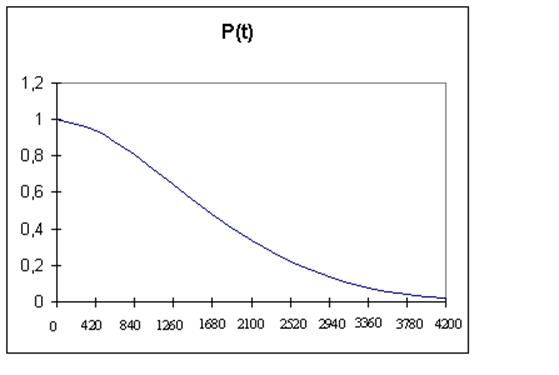
Представим теперь графически:

графики h(t), f(t), P(t)

Задача№3

На надежность отправления поездов по графику оказывают влияние 7 комплексов:

1          Локомотивный

2          Вагонный

3          Комплекс пути

4          Сигнализация и связь

5          Грузовой

6          Пассажирский

7          Комплекс формирования

Требуется определить общий коэффициент готовности отправления поездов по графику. При этом для каждого комплекса заданы средние времена наработки на отказ и восстановления.

Коэффициент готовности отправления по графику определяем по формуле:

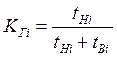
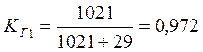
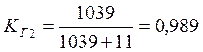
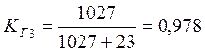
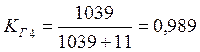
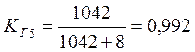
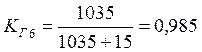
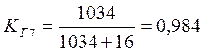
Определяем общий коэффициент готовности отправления поездов по графику:

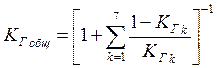
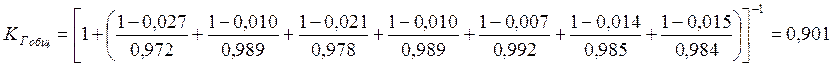
Задача№4