Система состоит из пяти элементов, соединенных как показано на рисунке. Предполагается, что элементы функционируют независимо. Система будет работоспособна, если между точками А и В можно построить цепь из работоспособных элементов. Предполагается, что все элементы идентично, среднее время наработки на отказ каждого элемента tср=150∙8=1200, время наработки имеет показательное распределение. Необходимо определить среднее время наработки на отказ всей системы.
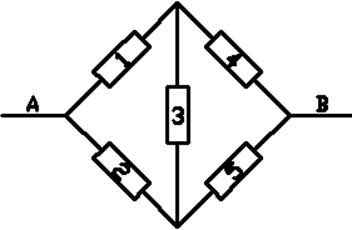
Таблица истинности:
|
1 |
2 |
3 |
4 |
5 |
Ф(x) |
P |
|
0 |
0 |
0 |
0 |
0 |
0 |
Qi5 |
|
0 |
0 |
0 |
0 |
1 |
0 |
PiQi4 |
|
0 |
0 |
0 |
1 |
0 |
0 |
PiQi4 |
|
0 |
0 |
0 |
1 |
1 |
0 |
Pi2Qi3 |
|
0 |
0 |
1 |
0 |
0 |
0 |
PiQi4 |
|
0 |
0 |
1 |
0 |
1 |
0 |
Pi2Qi3 |
|
0 |
0 |
1 |
1 |
0 |
0 |
Pi2Qi3 |
|
0 |
0 |
1 |
1 |
1 |
0 |
Pi3Qi2 |
|
0 |
1 |
0 |
0 |
0 |
0 |
PiQi4 |
|
0 |
1 |
0 |
0 |
1 |
1 |
Pi2Qi3 |
|
0 |
1 |
0 |
1 |
0 |
0 |
Pi2Qi3 |
|
0 |
1 |
0 |
1 |
1 |
1 |
Pi3Qi2 |
|
0 |
1 |
1 |
0 |
0 |
0 |
Pi2Qi3 |
|
0 |
1 |
1 |
0 |
1 |
1 |
Pi3Qi2 |
|
0 |
1 |
1 |
1 |
0 |
1 |
Pi3Qi2 |
|
0 |
1 |
1 |
1 |
1 |
1 |
Pi4Qi |
|
1 |
0 |
0 |
0 |
0 |
0 |
PiQi4 |
|
1 |
0 |
0 |
0 |
1 |
0 |
Pi2Qi3 |
|
1 |
0 |
0 |
1 |
0 |
1 |
Pi2Qi3 |
|
1 |
0 |
0 |
1 |
1 |
1 |
Pi3Qi2 |
|
1 |
0 |
1 |
0 |
0 |
0 |
Pi2Qi3 |
|
1 |
0 |
1 |
0 |
1 |
1 |
Pi3Qi2 |
|
1 |
0 |
1 |
1 |
0 |
1 |
Pi3Qi2 |
|
1 |
0 |
1 |
1 |
1 |
1 |
Pi4Qi |
|
1 |
1 |
0 |
0 |
0 |
0 |
Pi2Qi3 |
|
1 |
1 |
0 |
0 |
1 |
1 |
Pi3Qi2 |
|
1 |
1 |
0 |
1 |
0 |
1 |
Pi3Qi2 |
|
1 |
1 |
0 |
1 |
1 |
1 |
Pi4Qi |
|
1 |
1 |
1 |
0 |
0 |
0 |
Pi3Qi2 |
|
1 |
1 |
1 |
0 |
1 |
1 |
Pi4Qi |
|
1 |
1 |
1 |
1 |
0 |
1 |
Pi4Qi |
|
1 |
1 |
1 |
1 |
1 |
1 |
Pi5 |
Задача№5
На сортировочную станцию, имеющую 6 путей для переработки, прибывает в среднем 72 состава в сутки. Горочный технологический интервал составляет 15 мин. Определить среднее количество составов ожидающих расформирования. Поток поступающих составов считать простейшим; время расформирования – распределённым экспоненциально; технический процесс – стационарным.
При работе 6-ти бригад
рассматриваемая система представляет собой
. при этом
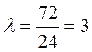состава/час;
Т.к.средняя продолжительность осмотра
состава 
0.25 ч., интенсивность обслуживания
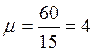состава/час;
Следовательно
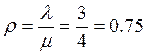
Среднее количество составов, ожидающих расформирования
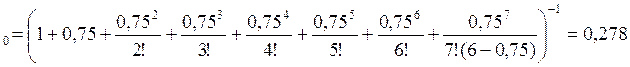
p
p
p
p
p
p
p
p
|
k |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
P |
0.487 |
0.156 |
0.117 |
0.088 |
0.066 |
0.049 |
0.037 |
Ответ: Среднее количество составов, ожидающих расформирования = 1.387.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.