Иногда на практике приходится иметь дело с явлениями, протекание которых во времени непредсказуемо и в каждый момент времени описывается случайной величиной. Такие явления называются случайными процессами.
Случайным процессом называется функция z(t) неслучайного аргумента t (как правило, времени), которая при каждом фиксированном значении аргумента является случайной величиной. Например, температура в течение суток, регистрируемая самописцем; значение уровня помехи во времени; количество посетителей в магазине в течение рабочего дня; население Земли.
Значения, принимаемые процессом z(t) в определенные моменты времени называются состояниями, а множество всех состояний – фазовым пространством случайного процесса. В зависимости от количества возможных состояний случайного процесса его фазовое пространство может быть дискретным (конечным или счетным) или непрерывным (несчетным).
Если случайный процесс может изменять свое состояние лишь в определенные (фиксированные) моменты времени, то такой процесс называется случайным процессом с дискретным временем; а если в произвольные, то – процессом с непрерывным временем.
Примеры траекторий случайных процессов приведены на рисунке 44.
а) 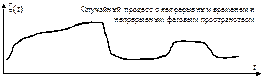 б)
б) 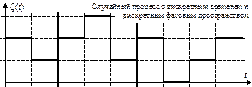
в) 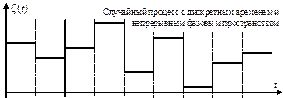
Рисунок 44 – Примеры траекторий случайных процессов
Пример 34
z(t) – число на кости при ежесекундном подбрасывании (случайный процесс с дискретным временем и дискретным фазовым пространством);
z(t) – количество подключений к Internet-серверу во времени (случайный процесс с непрерывным временем и дискретным фазовым пространством);
z(t) – температура окружающей среды, регистрируемая каждый час (случайный процесс с дискретным временем и непрерывным фазовым пространством); регистрируемая постоянно (случайный процесс с непрерывным временем с непрерывным фазовым пространством);
z(t) – состояние микропроцессора, как синхронного дискретного устройства (случайный процесс с дискретным временем и дискретным фазовым пространством). ¨
Случайный процесс z(t) называется стационарным, если распределение вероятностей его возможных состояний не изменяется во времени. Например, при ежесекундном подбрасывании игральной кости распределение вероятностей состояний соответствующего случайного процесса (см. рисунок 44, б) не зависит (не изменяется) от времени (в данном случае все состояния процесса z(t) равновозможны). В противоположность этому, случайный процесс, характеризующий температуру окружающей среды, не является стационарным, т.к. для лета характерны более высокие температуры, чем для зимы.
Распределение вероятностей состояний стационарного случайного процесса называется стационарным распределением.
Марковским называется случайный процесс z(t), эволюция которого после произвольного момента времени t0 зависит только от состояния процесса в момент t0 и не зависит от предыдущего поведения процесса. Примером дискретного марковского процесса с дискретным фазовым пространством является детская игра «тише едешь – дальше будешь», в которой игроки бросают кость и перемещают фишки на соответствующее число клеток. В данной игре движение фишки после i-го шага не зависит от того, как и за какое число шагов фишка достигла текущего состояния, а определяется только текущим положением фишки и последующими бросками кости. Другим примером марковского процесса является координата броуновской частицы.
Символически определение марковского процесса можно сформулировать так:
P(Б | П Ç Н) = P(Б | Н), т.е. при фиксированном «прошлом» и «настоящем» «будущее» зависит только от «настоящего». Аналогично можно показать, что для марковских процессов при фиксированном «настоящем» «прошлое» и «будущее» независимы.
Потоком событий называется последовательность событий (как правило, однотипных), происходящих одно за другим через некоторые промежутки времени. Поток событий описывается набором величин x1 – времени до первого события потока, x2 – временем между первым и вторым событиями потока и т.д. до бесконечности (рисунок 45, а). Поток событий, по существу, является случайным процессом (с дискретным фазовым пространством), где z(t) – число событий потока, поступивших к моменту времени t (рисунок 45, б).
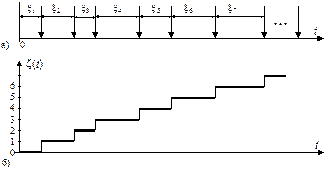
Рисунок 45 – Последовательность потока событий (а) и траектория, соответствующего случайного процесса (б)
Пример 35
Примерами случайных потоков являются: поток отказов ЭВМ, поток покупателей в магазин, поток заявок на АТС, поток студентов в гардероб, поток посещений Internet-сервера, поток электричек в метро, поток посетителей ЖД кассы (в часы ее работы) и т.д. ¨
Если величины xi , определяющие поток событий, являются случайными, то поток событий называется случайным, в противном случае поток событий называется регулярным (или детерминированным). В вероятностном смысле случайный поток событий описывается множеством совместных распределений случайных величин xi времени до первого события потока и между событиями (см. рисунок 45, а).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.