Элементы теории случайных процессов и случайных потоков, страница 5

Теорема о суперпозиции бесконечного числа независимых потоков событий. Поток событий, образованный суперпозицией бесконечного числа произвольных независимых рекуррентных потоков событий, является ППС с интенсивностью l_S » (M^–1[x₁]+M^–1[x₂] +…+ M^–1[x_i]+...), где M[x_i] – математическое ожидание времени между событиями  i-го потока событий.  ¨

Замечание – Примером практической значимости указанных теорем в теории надежности является то, что поток отказов системы, образованный потоками отказов компонентов системы, с увеличением числа компонентов приближается к простейшему потоку и характеризуется только интенсивностью (обратно пропорциональной математическому ожиданию времени безотказной работы системы), даже если потоки отказов компонентов системы не являются простейшими.  ¨

1.5.5 Прореживание простейших потоков событий

Возможны ситуации, когда не все события потока проходят через некоторое «решающее устройство» (рисунок 49). Например, не каждый посетитель магазина делает покупки, т.е. является посетителем кассы. Другой пример: не все отказы систем железнодорожной автоматики и телемеханики являются опасными. Некоторые из них являются защитными и могут быть своевременно устранены электромонтером.

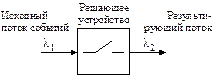
Рисунок 49 – Прореживание потока событий

Таким образом, лишь некоторые события исходного потока образуют результирующий поток событий. Часто встает задача определения характеристик результирующего потока событий исходя из характеристик первоначального потока и свойств «прореживающего устройства».

Если сквозь «решающее устройство» проходит строго каждое k-е событие (рисунок 50, а) исходного потока, то такое прореживание потока событий называется регулярным. Если же каждое из событий исходного потока проходит через «решающее устройство» с вероятностью P₀ (рисунок 50, б) и, соответственно, «задерживается» в нем с вероятностью (1–P₀), то такое прореживание называется случайным.  В случае регулярного прореживания (например каждого 2-го события, рисунок 50, а) время между событиями результирующего потока определяется суммой k величин времени между событиями исходного потока (рисунок 50, а).

а) 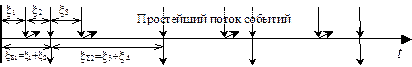 б)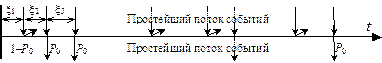 

Рисунок 50 – Прореживание простейшего потока событий: а – регулярное прореживание каждого второго события; б – случайное прореживание с вероятностью P₀

Если исходный поток является ППС с интенсивностью l, то время x_S между событиями результирующего потока есть  сумма  k  величин, имеющих показательный закон распределения с параметром l . В п. 1.2.12 указывалось, что случайная величина, подобная  x_S , имеет закон распределения Эрланга k-го порядка с параметром l .

Теорема о регулярном прореживании простейшего потока событий. Время x_S между событиями потока, образованного регулярным прореживанием ППС с интенсивностью l, когда пропускалось лишь каждое k-е событие исходного потока (), имеет закон распределения Эрланга k-го порядка с параметром l.  ¨

Теорема о случайном прореживании простейшего потока событий. Поток событий, образованный случайным прореживанием с вероятностью P₀ ППС с интенсивностью l₁ (см. рисунок 50, б), также является ППС с интенсивностью l₂ = l₁P₀ (т.е. с меньшей интенсивностью).

Следовательно, время между событиями потока, образованного случайным прореживанием ППС, имеет показательный закон распределения с математическим ожиданием (l₁P₀)^–1.  ¨