Пусть на некоторый объект воздействует n независимых ППС (рисунок 47). Например, поток отказов ЭВМ складывается из потока отказов процессора, памяти, системной платы, контроллеров, накопителей и прочего оборудования, а также программного обеспечения. Требуется определить характеристики результирующего потока событий.
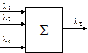
Рисунок 47 – Суперпозиция n простейших потоков событий
Рассмотрим эту задачу для случая двух исходных ППС: первый поток (рисунок 48, а) имеет интенсивность l1, а второй (рисунок 48, б) – интенсивность l2 . Пусть xij – время между (j–1) и j-м событиями i-го потока событий (см. рисунок 48, а,б).
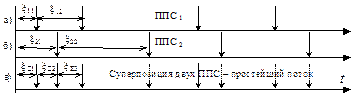
Рисунок 48 – Суперпозиция простейших потоков событий ППС1 и ППС2: а – простейший поток событий (ППС1); б – простейший поток событий (ППС2); в – суперпозиция двух простейших потоков событий (ППС)
Время xS1 до первого события потока, образованного суперпозицией двух потоков событий, очевидно из рисунка 48, в , равно минимальному из значений x11 и x21, т.е. xS1 = min{x11 , x21}. Поскольку ППС являются потоками без последействия, а также являются рекуррентными потоками, то время до очередного события результирующего потока-суперпозиции определяется соотношением:
xS = min{x1 , x2}, (81)
где xS – время между событиями результирующего потока событий; x1 – время между событиями 1-го ППС; x2 – время между событиями 2-го ППС.
Известно (см. замечание в п. 1.5.3), что x1 ~ E(l1), а x2 ~ E(l2). Следовательно, Fx1(x) = P(x1 < x) = 1–exp(–l1x), а Fx2(x) = P(x2 < x) = 1–exp(–l2x). Закон распределения случайной величины xS требует определения, т.е. FxS(x) = P(xS < x).
Рассмотрим вероятность события {xS ³ x}, противоположного к событию {xS < x}. P(xS ³ x) = P(min{x1 , x2} ³ x) = P({x1 ³ x} Ç {x2 ³ x}), поскольку чтобы меньшая из величин x1 , x2 была больше или равна x, необходимо, чтобы каждая из величин была больше или равна x.
Поскольку исходные потоки являются независимыми (по условию), то независимыми являются события {x1 ³ x} и {x2 ³ x}. Следовательно, применяя теорему умножения вероятностей для независимых событий, получим:
P(xS ³ x) = P({x1 ³ x} Ç {x2 ³ x}) = P(x1 ³ x) P(x2 ³ x) = = (1–P(x1 < x)) (1–P(x2 < x)) = (1–Fx1(x)) (1–Fx2(x)) = = (1–1+exp(–l1x)) (1–1+exp(–l2x)) = exp(–l1x) exp(–l2x) = exp(–(l1+l2) x).
Следовательно, FxS(x) = P(xS < x) = 1–P(xS ³ x) = 1–exp(–(l1+l2)x). Таким образом, время между событиями результирующего потока-суперпозиции имеет показательный закон распределения с параметром (l1+l2) (данный результат мог быть получен также с помощью предельной теоремы о минимальном среди значений показательно распределенных случайных величин (см. п. 1.4.2)), а поток событий, образованный суперпозицией двух простейших потоков с интенсивностями l1 и l2 , является ППС с интенсивностью (l1+l2).
Теорема о суперпозиции n независимых простейших потоков событий. Поток событий, образованный суперпозицией n независимых ППС с интенсивностями l1 , l2 ,…, ln , является ППС с интенсивностью lS = l1+ +l2+…+ln . Следовательно, время между событиями результирующего потока событий xS имеет показательный закон распределения с параметром lS и математическим ожиданием M[xS] = 1 / lS = 1 / (l1+l2+…+ln ). ¨
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.