Элементы теории массового обслуживания, страница 4

.                                                          (90)

Соотношения (86) и (90) устанавливают, что в бесконечно малом интервале времени число требований в системе M / M / 1 (а, следовательно, и состояние процесса z(t)) может измениться лишь на единицу. Кроме того, соотношения (86) и (90) определяют вероятности данных изменений. Представим граф перехода случайного процесса z(t), характеризующего число заявок в СМО в момент времени t (рисунок 54). Данный процесс часто называют в литературе процессом «размножения и гибели».

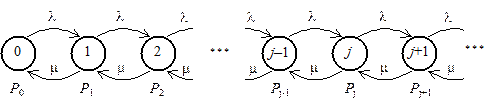
Рисунок 54 – Граф переходов процесса z(t), характеризующего число заявок в СМО M / M / 1

Определим вероятность того, что в некоторый момент времени t+Dt случайный процесс z(t) будет находиться в состоянии j , т.е. в СМО будет находиться j требований. При этом учтем, что в момент t в СМО первоначально могло находиться i требований. Тогда по формуле полной вероятности получаем уравнения, называемые уравнениями Чепмена-Колмогорова:

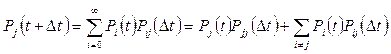.                       (91)

Здесь P_i(t) – вероятность гипотезы о том, что в момент времени t число заявок в системе равно i , i = 0, 1, 2, 3,…; P_ij(Dt) – вероятность того, что за время Dt число заявок в системе изменится с i до j. В правой части выражения (91) отдельно выделено слагаемое, для которого i = j.

Запишем уравнения Чепмена-Колмогорова (91) для всех состояний системы j = 0, 1, 2,…  при условии Dt®0. При этом также будем учитывать, что:

· P_i i+1(Dt) = P₊₁(Dt) = lDt , т.е. вероятность того, что за время Dt®0 число требований в СМО увеличится на единицу, равна lDt  по формуле (90);

· P_i i–1(Dt) = P_–1(Dt) = mDt  для i ³ 1, т.е. вероятность того, что за время Dt®0 число требований в СМО уменьшится на единицу при условии, что в начале рассматриваемого интервала времени число требований в системе больше нуля, равна mDt  по формуле (86);

· P_i i–1(Dt) = 0 для i = 0, т.е. вероятность того, что число требований в СМО станет отрицательным, равна нулю;

· P_ij(Dt) = 0 для |i–j| > 1, т.е. вероятность того, что за время Dt®0 число требований в СМО изменится более, чем на единицу, равна нулю;

· P_jj(Dt) = 1–(P_–1(Dt)+P₊₁(Dt)) для j ³ 1, т.е. вероятность того, что за время Dt®0 число требований в СМО не изменится, равна разности единицы и вероятностей того, что данное число уменьшится или увеличится на 1;

· P_jj(Dt) = 1–P₊₁(Dt) для j = 0, т.е. вероятность того, что за время Dt®0 число требований в СМО останется равным нулю, равна разности единицы и вероятности того, что число требований увеличится на единицу (поскольку данные события противоположны),

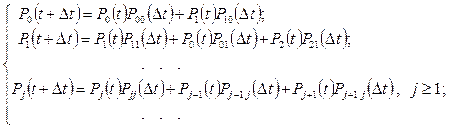
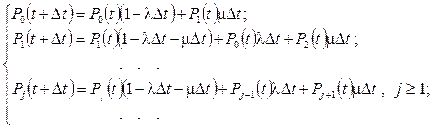
Перепишем полученную систему уравнений в виде:

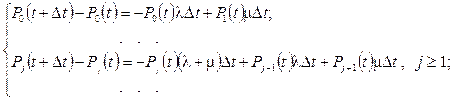
Разделим уравнения полученной системы на Dt в предположении, что Dt®0:

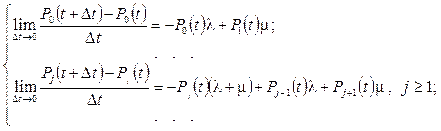
Учитывая, что в левых частях уравнений системы находятся производные, получим:

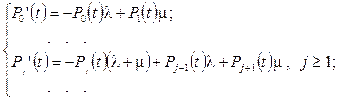                                (92)

Система дифференциальных уравнений Чепмена-Колмогорова (92) определяет вероятности состояний марковского процесса z(t), характеризующего число заявок в СМО M / M / 1, в произвольный момент времени t. Решение данной системы возможно с учетом условия нормировки

,                                                       (93)

определяющего вероятность суммы гипотез, а также с учетом начальных условий . Например, если в начальный момент времени (t = 0) в СМО отсутствовали заявки, то .