Элементы теории массового обслуживания, страница 9

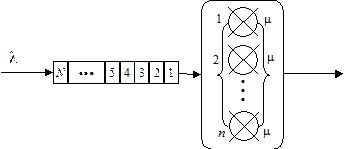
Рисунок 57 – Система массового обслуживания  M / M / n / N

Очевидно, что в СМО вида M / M / n / N одновременно может находится n+N требований. Очередное n+N+1 требование получает отказ в обслуживании. Граф переходов случайного процесса z(t), характеризующего число заявок в СМО M / M / n / N, представлен на рисунке 58. Видно, что при наличии в СМО M / M / n / N  j требований (0 £ j < n+N) интенсивность перехода процесса z(t) из состояния j в состояние j+1 равна интенсивности входящих требований l. А интенсивность перехода z(t) из состояния j в состояние j–1 (1 £ j £ n+N) равна суммарной интенсивности обслуживания требований, т.е. j m для j Î [1; n] и  n m  для j Î [n; N] (рисунок 58).

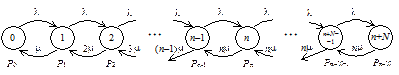
Рисунок 58 – Граф переходов процесса z(t), характеризующего число заявок в СМО M / M / n / N

Процесс z(t), характеризующий число требований в системе M / M / n / N, со временем стремится к стационарному режиму независимо от значений параметров l, m и начального распределения состояний процесса z(t). Распределение вероятностей числа требований в системе в стационарном режиме определяется выражением:

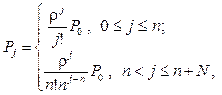                                                 (104)

где r = l / m , а .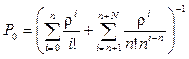

Отметим, что величина P_n+N определяет вероятность того, что очередной заявке будет отказано в обслуживании (ввиду занятости всех обслуживающих приборов и мест ожидания).

Математическое ожидание числа требований z в СМО M / M / n / N в стационарном режиме определяется выражением

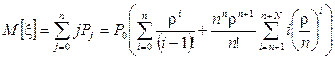 .                             (105)

Пример 40

В городской справочной службе работают 2 оператора. Абонент, который застает занятыми обоих операторов, подключается для ожидания к автоответчику. Как только один из операторов освобождается, ожидающая заявка переходит к нему на обслуживание, а автоответчик освобождается. Абонент, который застает занятыми операторов и автоответчик, получает отказ в обслуживании. В среднем за час в справочную службу обращаются 50 абонентов, а время обслуживания составляет в среднем 2 минуты.

Определить, как изменяется вероятность отказа в обслуживании абонента при использовании одного автоответчика. Кроме того, определить среднее время ожидания обслуживания, т.е. среднее время подключения к автоответчику.

При решении использовать допущения о том, что поток поступающих заявок является простейшим, а время обслуживания имеет показательный закон распределения. Предполагается, что абонент, подключенный для ожидания к автоответчику, не покидает систему. Следует также пренебречь повторными вызовами (когда абонент, получивший отказ в обслуживании, повторяет свой запрос).

Решение. По условию интенсивность простейшего входящего потока l, определяемая выражением (79), равна 50 заявок / ч. А интенсивность обслуживания обратно пропорциональна среднему времени обслуживания (см. выражение (83)) и составляет m = 1 / M[t] = 1 / 2 заявок / мин или 30 заявок / ч. Поскольку в справочной работают два оператора, а при занятых операторах один абонент, подключаясь к автоответчику, ожидает обслуживания, то рассматриваемую систему можно классифицировать как СМО вида M / M / 2 / 1.

Распределение вероятностей числа заявок, обслуживаемых в системе, определим по формуле (104), где r = l / m = 50 / 30 = 5 / 3 :

 ;    ;

 .

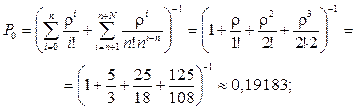
Результаты вычислений сведем в таблицу 10.

Таблица 10 – Ряд распределения числа требований в справочной службе M / M / 2 / 1