Элементы теории массового обслуживания, страница 5

Особое значение имеет определение стационарного распределения вероятностей пребывания СМО в одном из возможных состояний. В теории массового обслуживания доказывается, что при любом начальном распределении состояний процесса z(t) (), характеризующего СМО M / M / 1, он будет со временем стремиться к стационарному распределению (а сам процесс z(t) будет стационарным) в случае, если m > l, т.е. интенсивность обслуживания будет превышать интенсивность входящего потока требований. Интуитивно понятно, что если m £ l, то обслуживающий прибор перестанет справляться с поступающими требованиями, число требований в очереди (и в системе в целом) будет постоянно увеличиваться.

Режим работы СМО, при котором процесс z(t), характеризующий число требований в системе, будет стационарным, называется стационарным режимом.

Пример 37

Рассмотрим, например, работу билетной кассы как СМО вида M / M / 1. В начале рабочего дня число требований (посетителей) в данной СМО равно нулю, а начальное распределение вероятностей числа посетителей в системе: . Со временем число посетителей в кассе увеличивается, но не бесконечно. Как правило, после нескольких часов работы в билетной кассе можно застать от 2 до 5 человек, из которых 1–4 посетителя находятся в очереди. К концу рабочего дня данная ситуация практически не изменяется.

В действительности можно застать ситуации неэффективной работы билетных касс (длительный простой кассира или, напротив, значительное увеличение длины очереди), которые обусловливаются тем, что в реальности нарушаются допущения о простейшем входящем потоке требований (с постоянной интенсивностью l) и о показательном распределении времени обслуживания каждого посетителя.

Вместе с тем, даже в подобных случаях, использование простейших марковских моделей теории массового обслуживания предоставляет достаточно точные результаты, поэтому марковские модели часто используются для предварительных оценочных расчетов характеристик реальных СМО.  ¨

Поскольку вероятности состояний стационарного процесса не изменяются во времени, то , а левые части уравнений системы (92) равны нулю: . В этом случае система уравнений (92) с учетом ограничения (93) запишется следующим образом:

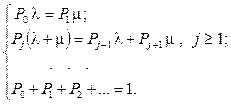                                                  (94)

Вычитая из второго уравнения системы (94) (для j = 1) первое уравнение (для j = 0), получим:

Вычитая полученное выражение из третьего уравнения системы (94) (для j = 2), получим:

Продолжая этот процесс далее, система уравнений (94) преобразуется в систему:

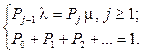
Таким образом, вероятность пребывания СМО j-м состоянии (нахождения в системе j требований) определяется через вероятность нулевого состояния (когда в системе нет требований) с помощью соотношения:

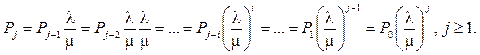         (95)

Подставляя значения вероятностей , выраженные через P₀ , в последнее уравнение системы (94), получим ее решение:

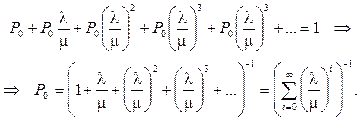
Поскольку m > l, то сумма геометрической прогрессии 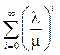сходится к 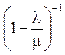. Следовательно, вероятность того, что СМО вида M / M / 1 в произвольный момент работы (в стационарном режиме) будет простаивать, равна:

.                                                                    (96)

Отношение l / m в формуле (96), определяющее вероятность того, что в СМО вида M / M / 1 находится хотя бы одна заявка (т.е. обслуживающий прибор занят), называется коэффициентом загрузки системы M / M / 1 и обозначается r .

Таким образом, вероятность того, что в СМО вида M / M / 1 (в стационарном режиме работы) находится j требований, определяется только коэффициентом загрузки системы r в соответствии с выражением (95) с помощью соотношения:

,                                                                 (97)

а величина z = z(t), характеризующая число требований в стационарном режиме работы СМО M / M / 1, имеет геометрический закон распределения (39) с параметром p = (1–r) (см. п. 1.2.9).