Элементы теории массового обслуживания, страница 7

Определим коэффициент загрузки r системы M / M / 1, который характеризует вероятность того, что в произвольный момент времени кассир будет занят, по формуле (96):

.

Вероятности того, что в произвольный момент времени (в стационарном режиме) в кассе будет находиться j посетителей, определим по формуле (97):

;

;

;

;

;

;

;

.

Результаты расчетов первых восьми вероятностей сведем в таблицу 8.

Таблица 8 – Ряд распределения числа посетителей в билетной кассе

Видно, что вероятности пребывания в кассе j посетителей убывают с ростом числа j. Наиболее вероятно, что посетители в кассе отсутствуют.

Вероятность того, что число посетителей в кассе превысит 5 человек, определим через вероятность противоположного события из соотношения:

P_>5 = 1–(P₀+P₁+P₂+P₃+P₄+P₅) = 1–0,91221 = 0,08779 .

Определим среднее число посетителей в кассе z в стационарном режиме ее работы по формуле (98):

M[z] = r / (1–r) = (2 / 3) / (1–2 / 3) = 2 чел., т.е. в среднем в помещении данной билетной кассы находится два человека.

Математическое ожидание числа требований на обслуживающем приборе определим по формуле (98):

M[n] = r = 2 / 3 » 0,6666 чел.

Математическое ожидание числа посетителей, находящихся в очереди перед кассой, определяется выражением (99):

M[h] = r² / (1–r) = (2 / 3)² / (1–2 / 3) = 4 / 3 » 1,3333 чел., т.е. в очереди перед кассой можно застать в среднем 1,3333 человек.

Математические ожидания времени пребывания посетителей в системе V и времени ожидания посетителей в очереди W, определим по формулам Литтла (100):

M[V] = M[z] / l = 2/(1/3) = 6 мин;  M[W] = M[h] / l = (4 / 3) / (1 / 3) = 4 мин, т.е. в среднем каждый посетитель тратит на приобретение билета 6 минут, из которых в среднем 4 минуты он проводит в ожидании обслуживания.  ¨

1.6.4 Система M / M / n / 0 (задача Эрланга)

Рассмотрим систему массового обслуживания вида M / M / n / 0 – n канальную марковскую СМО с потерями (рисунок 55).

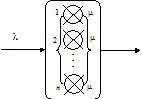
Рисунок 55 – Система массового обслуживания  M / M / n / 0

Примером подобной системы является работа АТС, которая способна одновременно обслуживать не более n своих абонентов; а также пейджинговая служба, в которой одновременно работает n операторов. При этом n+1 абонент АТС (пейджинговой службы) получает отказ в обслуживании, т.к. данная СМО не имеет очереди. Интенсивность входного простейшего потока требований равна l, а время обслуживания требований каждым из n приборов имеет показательный закон распределения с параметром m .

Случайный процесс z(t), характеризующий число требований в системе M / M / n / 0 в момент времени t, является марковским процессом, а граф его состояний представлен на рисунке 56. Интуитивно понятно, что при наличии в СМО M / M / n / 0 j требований (0 £ j < n) интенсивность перехода процесса z(t) из состояния j в состояние j+1 равна интенсивности входящих требований l. А интенсивность перехода z(t) из состояния j в состояние j–1 (1 £ j £ n) равна суммарной интенсивности обслуживания j требований, т.е. j m (рисунок 56).

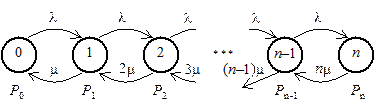
Рисунок 56 – Граф переходов процесса z(t), характеризующего число заявок в СМО M / M / n / 0