Элементы теории массового обслуживания, страница 10

Из таблицы 10 видно, что наиболее вероятно, что в стационарном режиме в СМО находится лишь одно требование, т.е. занят один из операторов. Вероятность того, что абонент будет ожидать обслуживания, подключившись к автоответчику, равна 0,22205. С такой же вероятностью очередной абонент получит отказ в обслуживании, т.е. P_отказа = 0,22205.

Сравним полученное значение вероятности отказа с вероятностью отказа в обслуживании системой M / M / 2 / 0 (т.е. когда не используется автоответчик) по формуле (102):

 .

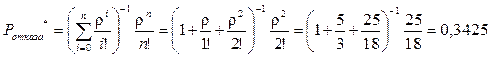Видно, что использование автоответчика, как «места» для ожидания обслуживания, позволяет существенно уменьшить вероятность отказа в обслуживании абонентов справочной службы.

Для определения среднего времени ожидания обслуживания рассмотрим случайную величину h – число требований в очереди, которая принимает значение 0, если в СМО M / M / 2 / 1 находится не более двух требований (обслуживаемых операторами). Величина h = 1, если в системе находятся 3 требования (одно из которых ожидает обслуживания, подключаясь к автоответчику). Ряд распределения величины h приведен в таблице 11.

Таблица 11 – Ряд распределения числа требований, ожидающих обслуживания

Определим математическое ожидание дискретной случайной величины  h  по формуле (28):

M[h] = 0×0,77795+1×0,22205 = 0,22205 .

Математическое ожидание случайной величины W, характеризующей время ожидания требованиями своего обслуживания, определяется по формуле Литтла (100):

W = M[h] / l = 0,22205 / 50 = 0,004441 ч  или 16 с.

Таким образом, абонент, который застал обоих операторов занятыми и был подключен к автоответчику, будет ожидать начала своего обслуживания в среднем 16 с.  ¨

1.6.6 Система M / M / n

Рассмотрим СМО M / M / n, аналогичную системе M / M / n / N, (см. рисунок 57) в которой, однако, число мест в очереди не ограничено (т.е. N = ¥). В теории массового обслуживания доказывается, что распределение вероятностей числа требований z(t) в системе M / M / n при любом начальном распределении со временем будет стремиться к стационарному распределению (не изменяющемуся во времени: ) при условии l < nm, т.е. когда интенсивность входящего потока меньше суммарной интенсивности обслуживания требований n приборами СМО. В противном случае, очередь требований, ожидающих обслуживания будет постоянно расти.

В стационарном режиме работы распределение вероятностей числа требований в системе z определяется соотношениями:

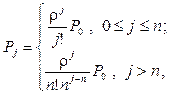                                                         (106)

где r = l / m , а .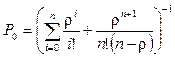

Вероятность того, что в СМО M / M / n будут заняты все приборы,

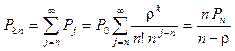 .                                              (107)

Математическое ожидание числа занятых обслуживающих приборов

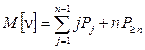 .                                                             (108)

Математическое ожидание числа требований, ожидающих обслуживания в очереди,

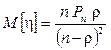 .                                                                   (109)

Математическое ожидание числа требований в системе

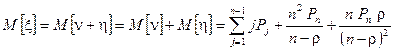 .                   (110)

Математические ожидания времени пребывания требований в СМО M / M / n (включая ожидание и обслуживание) V, а также времени ожидания в очереди W определяются по формулам Литтла (100).