Элементы теории массового обслуживания, страница 8

Процесс z(t), определяющий число требований в системе M / M / n / 0, со временем переходит в стационарный режим независимо от начального распределения процесса z(t) и значений параметров l и m. А распределение вероятностей числа требований в системе в стационарном режиме определяется выражением, называемым формулой Эрланга,

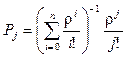,  j =  ,                                                      (101)

где r = l / m .

В частности, вероятность того, что очередной заявке будет отказано в обслуживании (вследствие занятости всех обслуживающих приборов)

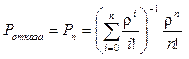 .                                                      (102)

В стационарном режиме работы математическое ожидание дискретной величины z числа требований в системе M / M / n / 0 (т.е. числа занятых обслуживающих приборов) определяется в соответствии с (28) выражением:

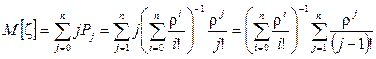 .                       (103)

Пример 39

В пейджинговую службу, в которой работают 5 операторов, поступает в среднем 45 заявок в час. На обслуживание каждой заявки уходит в среднем 4 минуты. Предполагая, что поток поступающих заявок является ППС, а время обслуживания имеет показательный закон распределения, определить вероятность отказа в обслуживании (ввиду занятости всех операторов), а также среднее число занятых операторов службы. При анализе следует пренебречь повторными заявками, когда абонент, получивший отказ в обслуживании, повторяет попытку дозвониться.

Решение. По условию интенсивность входящего потока l равна 45 заявок / ч. А интенсивность обслуживания обратно пропорциональна среднему времени обслуживания, определяемому выражением (83), и составляет m = 1 / M[t] = 1 / 4 заявок / мин или 15 заявок / ч. Поскольку в пейджинговой службе работает пять операторов (независимых обслуживающих приборов), а требования, которые застают всех операторов занятыми, остаются не обслуженными, то рассматриваемую систему можно классифицировать как СМО вида M / M / 5 / 0.

Распределение вероятностей числа заявок, обслуживаемых в системе, определим по формуле (101), где r = l / m = 45 / 15 = 3:

 ;

 ;

. . .

 .

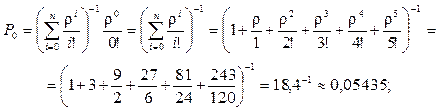
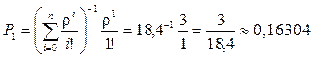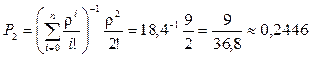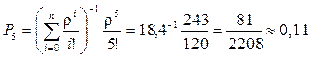Результаты вычислений сведем в таблицу 9.

Таблица 9 – Ряд распределения числа занятых операторов пейджинговой службы

Из таблицы 9 видно, что наиболее вероятным числом занятых операторов является 2 и 3.  А вероятность отказа в обслуживании очередного требования  P_отказа = P₅ = 0,11 .

Математическое ожидание числа занятых операторов пейджинговой службы определим по формуле (103):

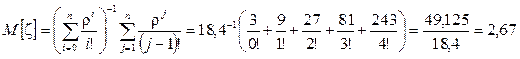, т.е. в стационарном режиме работы пейджинговой службы в среднем занято 2,67 оператора из пяти.  ¨

Замечание – Выражения (101)–(103) справедливы и для СМО вида M / G / n / 0, когда время обслуживания требований t имеет произвольный закон распределения. При этом параметр СМО r определяется через математическое ожидание t с помощью выражения: r = M[t] l .  ¨

1.6.5 Система M / M / n / N

Рассмотрим систему массового обслуживания вида M / M / n / N – n канальную марковскую СМО, в которой имеется N мест для ожидания обслуживания (рисунок 57). Интенсивность входного простейшего потока требований равна l, а время обслуживания требований каждым из n обслуживающих приборов имеет показательный закон распределения с параметром m . Примером подобных систем являются справочные и пейджинговые службы, в которых заявка, которая застает занятыми все обслуживающие приборы, переключается для ожидания к одному из N автоответчиков.