Элементы теории массового обслуживания, страница 3

· P_–0(Dt) – вероятность того, что за время Dt системой M / M / 1  не было завершено обслуживание ни одного из требований, находящихся в системе в начале рассматриваемого интервала времени;

· P_–1(Dt) – вероятность того, что за время Dt системой M / M / 1 было обслужено одно требование, находящееся в системе в начале рассматриваемого интервала времени;

· P_ij(Dt) – вероятность того, что за время Dt число заявок в системе M / M / 1 изменилось с i до j , i, j ³ 0.

Определим вероятность (1–P_–0(Dt)) того, что за время [t , t+Dt) системой будет обслужено хотя бы одно требование, находящееся в СМО. Указанная вероятность, по существу, состоит в том, что величина t времени обслуживания системой одного требования будет принадлежать интервалу [t ; t+Dt):

,                                             (84)

где t ~ E(m), а условие t ³ t  указывает на то, что требование уже находилось на обслуживании по крайней мере время t. При этом, в силу свойства «отсутствия памяти» у показательного распределения, не важно, сколько времени к моменту t требование находилось на обслуживании в марковской системе.

При условии, что Dt®0, выразим вероятность в левой части равенства (84) через определение интенсивности обслуживания (82):

.

Учитывая, что интенсивность обслуживания в СМО вида M / M / 1 постоянна и равна m, вероятность обслуживания СМО хотя бы одной заявки в интервале времени Dt®0 (при условии, что в начале рассматриваемого времени обслуживающий прибор был занят) определяется выражением:

.                                      (85)

Если бы обслуживающий прибор СМО никогда не простаивал, то в силу показательного закона распределения длительности обслуживания, поток обслуженных требований являлся бы простейшим (см. замечание в п. 1.5.3). А поскольку ППС является ординарным (т.е. вероятность поступления двух и большего числа событий в бесконечно малом интервале времени пренебрежимо мала по сравнению с вероятностью поступления только одного события), то вероятностью обслуживания системой в бесконечно малом интервале времени двух или большего числа требований можно пренебречь. Следовательно,

.                                                          (86)

Таким образом, вероятность того, что в интервале времени [t ; t+Dt) (при Dt®0) системой будет обслужено одно требование, находящееся в момент t в системе, равна вероятности обслуживания хотя бы одного требования и равна произведению интенсивности обслуживания на величину Dt.

Определим вероятность того, что в интервале времени [t ; t+Dt) в систему поступит хотя бы одно требование. Указанная вероятность, по существу, состоит в том, что величина x времени между поступающими заявками будет принадлежать интервалу [t ; t+Dt):

,                                            (87)

где x ~ E(l), а условие x ³ t  указывает на то, что к началу рассматриваемого интервала времени требование в СМО еще не поступило. По свойству «отсутствия памяти» у показательного распределения (47), указанная в формуле (87) условная вероятность равна безусловной:

.

Поскольку x ³ 0, то, воспользовавшись определением функции показательного распределения, получаем:

.                                      (88)

Разложим правую часть выражения (88) в ряд Маклорена

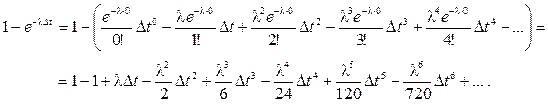
Можно доказать, что в пределе Dt®0 сумма указанного знакопеременного бесконечного ряда равна его первому слагаемому, то есть

.

Таким образом, вероятность поступления в СМО хотя бы одной заявки в интервале времени [t ; t+Dt) при Dt®0 определяется выражением

.                                      (89)

Поскольку входящий в систему M / M / 1 поток требований является ординарным, то вероятность поступления (в интервале времени Dt®0) в СМО хотя бы одного требования равна вероятности поступления только одного требования (вероятностью поступления в систему двух и большего числа требований при Dt®0 можно пренебречь). Следовательно, при Dt®0