Элементы теории массового обслуживания, страница 2

Интенсивностью m(t) обслуживания требований в момент t называется предел отношения условной вероятности того, что в интервале времени [t , t+Dt) закончится обслуживание требования, находящегося на обслуживании по крайней мере время t, к длительности указанного интервала при его стремлении к нулю. Если t – время обслуживания требования, находящегося в обслуживающем приборе, с функцией распределения F(t) и функцией плотности распределения f(t), то, проводя цепочку рассуждений, аналогичную выражениям (77) и (78), получим:

.                                    (82)

Так, например, если время обслуживания требований t имеет показательный закон распределения с параметром l₀  (т.е. t ~ E(l₀)), то интенсивность обслуживания от времени не зависит и равна значению параметра показательного распределения l₀ , т.е. обратно пропорциональна математическому ожиданию времени обслуживания требований M[t]:

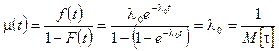 .                                         (83)

1.6.2 Понятие о марковских системах массового обслуживания

Рассмотрим случайный процесс z(t), который характеризует число требований в СМО в момент времени t. Очевидно, что данный процесс является случайным процессом с непрерывным временем и дискретным фазовым пространством (рисунок 52).

Рисунок 52 – Пример эволюции случайного процесса z(t), характеризующего число требований в СМО

Вероятностная эволюция процесса z(t) определяется:

1) числом требований в СМО в момент t₀, т.е. текущим состоянием процесса z(t);

2) моментами поступления требований в СМО после момента t₀;

3) моментами окончания обслуживания требований после момента времени t₀ (см. рисунок 52).

У систем вида  M / M / n / N (n ³ 1, N ³ 0) входной поток является простейшим, следовательно, (из-за отсутствия последействия) моменты поступления требований после момента t₀ не зависят от предыстории СМО. А поскольку время обслуживания имеет показательный закон распределения, то (по свойству «отсутствия памяти») время завершения обслуживания заявки, находящейся в обслуживающем приборе, не зависит от того, сколько времени данная заявка уже обслуживалась к моменту t₀.

Таким образом, для систем вида  M / M / n / N (n ³ 1, N ³ 0) вероятностная эволюция процесса z(t) после момента времени t₀ не зависит от эволюции процесса z(t) до момента t₀ , а определяется только текущим состоянием процесса z(t). Следовательно, процесс z(t), определяющий число требований в системе вида M / M / n / N в момент t, является марковским, а указанные СМО называются марковскими системами массового обслуживания.

1.6.3 Определение характеристик системы M / M / 1 (M / M / 1 / ¥)

Рассмотрим наиболее простую СМО – одноканальную марковскую систему с ожиданием типа M / M / 1 (рисунок 53). Интенсивность входного простейшего потока требований равна l, а время обслуживания каждого требования имеет показательный закон распределения с параметром m .

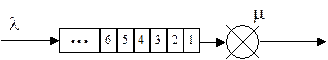
Рисунок 53 – Система массового обслуживания  M / M / 1

Условимся о следующих обозначениях:

· x – случайная величина времени между поступающими в систему требованиями, x ~ E(l);

· t – случайная величина времени обслуживания требований в СМО, t ~ E(m);

· z(t) – случайный процесс, характеризующий число требований в СМО в момент времени t;

· P_j(t) – вероятность того, что в момент времени t число заявок в системе M / M / 1  равно j , j ³ 0;

· P_+k(Dt) – вероятность того, что за время Dt в систему поступило k требований;

· P₊₀(Dt) – вероятность того, что за время Dt в систему требования не поступали;